P-n-переход при подаче внешнего напряжения

Рассчитаем прямой и обратный токи p-n-перехода, исходя из основных процессов в базе диода. Будем по-прежнему считать, что концентрация донорной примеси в эмиттере N_D = n_n значительно превышает концентрацию акцепторной примеси в базе N_A = p_p. В этом случае и при прямом и при обратном напряжении можно учитывать только электронную составляющую тока i = i_n + i_p » i_n .

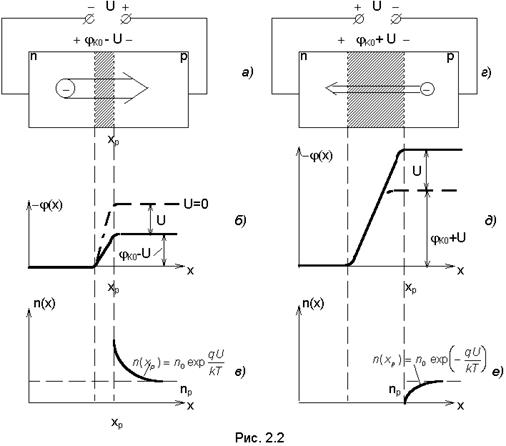
В самом деле, при прямом напряжении прямой ток определяется потоком основных носителей заряда, а т.к. n_n » p_p , то дырочной составляющей прямого тока можно пренебречь. При обратном напряжении обратный ток определяется потоком неосновных носителей заряда; поскольку

,

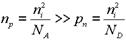то и в этом случае дырочной составляющей обратного тока можно пренебречь.

Рассматривая процессы в p-n-переходе при подаче внешнего напряжения будем так же полагать, что сопротивление обедненной области, где подвижных носителей заряда практически нет, значительно больше, чем сопротивление областей n- и p-типа вне перехода. Это допущение позволит считать, что все внешнее напряжение падает на p-n-переходе и контактная разность потенциалов соответственно изменяется до величины j_K0±U, где знак “-” соответствует падению потенциального барьера вследствие подачи прямого напряжения на p-n-переход, а знак “+” - при подаче обратного напряжения(см. рис.2.2,а).

Распределение потенциала вдоль структуры p-n-перехода показано на рис.2.2,б.

При прямом напряжении (U >0) уменьшение потенциального барьера приводит к преобладанию потока электронов из эмиттера в базу (ПОНЗ) над потоком электронов из базы в эмиттер (ПННЗ). При этом электроны инжектируются в базу и концентрация электронов на границе x_p возрастает до величины

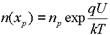, которая уже при U=0,26 В ( 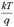=0,026В)

значительно превышает равновесную концентрацию в базе. Таким образом, инжекция электронов в базу приводит к появлению неравновесных носителей в базе Dn(x_p) = n (x_p) - n_p . Вследствие возникшего градиента концентрации в базе начинается процессдиффузии электронов от границы перехода x_p в глубину p-базы. По мере движения неравновесная концентрация уменьшается за счет рекомбинации.

Таким образом, три процесса определяют распределение неравновесной концентрации в базе p-n-перехода при прямом напряжении:

- инжекция - вызывает увеличение граничной концентрации n(x_p), то есть приводит к появлению неравновесных носителей заряда в базе;

- диффузия - является причиной движения электронов (ННЗ) через базу;

- рекомбинация - приводит к уменьшению неравновесной концентрации в базе вдали от p-n-перехода.

Распределение концентрации электронов в базе показано на рис. 2.2,в, оно описывается уравнением (1.34)

,

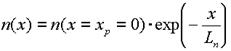где n(x=x_p=0) - граничная концентрация ,

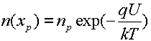
L_n -диффузионная длина электронов в базе.

Прямой электронный ток через p-n-переход может быть определен в любом сечении двухэлектродной структуры, однако удобнее это сделать в сечении x_p, где задана граничная концентрация .электронов

По своей природе электронный ток в сечении x_p является диффузионным и может быть рассчитан по формуле (1.44)

,

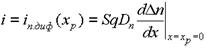где S - площадь p-n-перехода, q - заряд электрона, D_n - коэффициент диффузии электронов.

С учетом

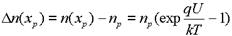
прямой ток p-n- перехода определяется выражением:

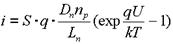. (2.5)

Обозначим 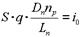, эта величина имеет размерность тока, определяется концентрацией неосновных носителей заряда в базе n_p и называется тепловым током i₀.

Проведя аналогичные рассуждения для обратного смещения, отметим следующее: p-n-переход при обратном смещении экстрагирует (выводит) электроны из базы. Граничная концентрация уменьшается по сравнению с равновесной и определяется выражением:

,

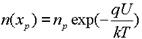которое отличается от соответствующего выражения при прямом напряжении полярностью напряжения U в экспоненте.

Три процесса определяют обратный ток p-n-перехода:

- экстракция электронов из базы;

- диффузия их из глубины базы к границе перехода x_p;

- генерация пар электрон - дырка в областях, где n(x)<n_p.

Распределение потенциала j(x) и концентрации n(x) для обратного напряжения приведены на рис. 2.2 г,д,е - правый столбец.

Вывод выражения для электронной составляющей обратного тока через p-n-переход полностью аналогичен выводу прямого тока.

Выражение для электронной составляющей обратного тока отличается от (2.5) только знаком внешнего напряжения и имеет вид :

.

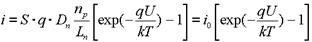Таким образом, ВАХ p-n-перехода описывается выражением

,

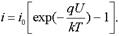где i₀ - тепловой ток p-n-перехода, с учетом дырочной составляющей тепловой ток может быть записан в виде:

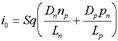. (2.6)

Тепловой ток p-n-перехода определяется потоками ННЗ и зависит от концентрации примеси ( так как n_p = n_i²/N_A; p_n = n_i²/N_D ) и температуры (так как: n_i²~ exp T² ).

Увеличение температуры p-n- перехода приводит к увеличению теплового тока, а, следовательно, к возрастанию прямого и обратного токов.

Увеличение концентрации легирующей примеси приводит к уменьшению теплового тока, а, следовательно, к уменьшению прямого и обратного токов p-n-перехода.

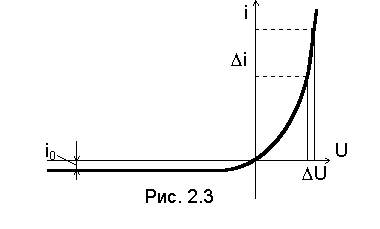
На рис. 2.3 построена ВАХ идеального p-n-перехода, полученного при принятых нами допущениях. При построении ВАХ примем T= 300К, тогда kT/q = 0,026В. Оценим прямой и обратный токи p-n перехода при подаче внешнего напряжения U=±0,26 В. При U=+0,26 В (прямое напряжение) (2.5) приводится к виду:

i = i₀• (exp 10 – 1) » i₀·exp 10 >> i₀

Таким образом, уже при U = 0,26 В величина прямого тока значительно превышает тепловой ток p-n перехода.

При U = - 0,26 В (обратное напряжение)

i = i₀ · (exp–10 – 1) » - i₀.

Таким образом, при обратном напряжении через p-n переход протекает тепловой ток i₀ , значение которого не зависит от величины приложенного обратного напряжения.

ВАХ p-n-перехода представляет собой нелинейную зависимость между током и напряжением. В общем случае к p-n-переходу может быть приложено как постоянное напряжение, определяющее рабочую точку на характеристике, так и переменное напряжение, амплитуда которого определяет перемещение рабочей точки по характеристике. Если амплитуда переменного напряжения мала, перемещение рабочей точки не выходит за пределы малого участка характеристики и его можно заменить прямой линией. Тогда между малыми амплитудами тока и напряжения (или между малыми приращениями тока и напряжения Di и Du) существует линейная связь. В этом случае p-n-переход на переменном токе характеризуют дифференциальным сопротивлением r_pn:

.

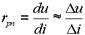Аналитическое выражение r_pn получим, дифференцируя (2.5)

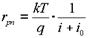
При прямом напряжении r_pn мало и составляет единицы - сотни ом, а при обратном напряжении - велико и составляет сотни и тысячи килоом.

Дифференциальное сопротивление можно определить графически по характеристике. (См. рис. 2.3, где указаны Du и Di).