Резонансні властивості паралельного та послідовного коливальних контурів

Отже і у паралельному коливальному контурі частотні характеристики в основному визначаються множником .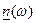

Універсальність цієї функції заслуговує більш детального аналізу її поведінки. Графічне зображення модуля 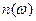називається резонансною кривою. Легко переконатися, що вхідний опір послідовного контуру (5.6), вхідний опір (5.14) та коефіцієнт передачі за напругою (5.17) паралельного контуру при малих втратах є резонансними кривими, оскільки визначаються 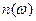помноженим на сталий коефіцієнт. Графік залежності

(5.18)

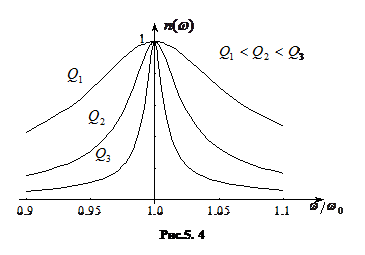при різних значеннях добротнності наведений на рис.5.4. Незалежно від добротності функція набуває максимального значення на резонансній частоті , тобто при 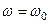, причому .

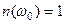Часто виникає необхідність знати фазовий зсув між напругою та струмом на вході коливального контуру. Така інформація міститься у вхідному імпедансі (у його аргументі). Тому для послідовного коливального контуру 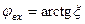, а для паралельного - 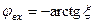. Фазочастотні характеристики послідовного та паралельного коливальних контурів при різних добротностях показані на рис.5.5.

Отримані раніше значення коефіцієнтів передачі за напругою для послідовного та паралельного коливальних контурів показують,що АЧХ та ФЧХ цих кіл при незначних втратах визначаються резонансними характеристиками. Якщо при цьому 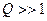, так що резонансна крива гостра, і слід до уваги брати лише вузький діапазон частот поблизу резонансної частоти ( 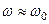), то для послідовного контуру

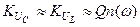, (5.19)

для паралельного контуру

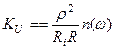. (5.20)

Отже, для усіх наведених випадків амплітудно-частотні характеристики коефіцієнтів передачі близькі до резонансних кривих відповідних контурів. При значних добротностях ці характеристики сильно залежать від частоти, і розглянуті кола виявляються вузькосмуговими. Звичайно ними не можна користуватися для неспотвореної передачі складного сигналу з широким спектром. Навпаки, їх зручно використовувати для виділення із складного сигналу деякої складової. Якщо на таке коло одночасно діють декілька сигналів різної частоти, наприклад сигнали передавачів декількох радіостанцій, то воно здатне виділити сигнал лише тієї радіостанції, частота якої співпадає з резонансною частотою контуру або близька до неї.

Знайдемо значення комплексних коефіцієнтів передачі для послідовного та паралельного коливальних контурів на резонансній частоті:

для послідовного контуру - 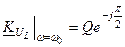, 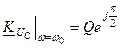; (5.21)

для паралельного - 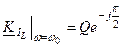, 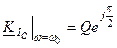. (5.22)

Таким чином на резонансній частоті напруга на реактивних елементах послідовного коливального контуру у 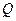разів перевищує вхідну напругу. Так, наприклад, якщо амплітуда вхідної напруги становить 1 В, то у послідовному контурі з добротністю 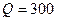напруга на конденсаторі буде рівною 300 В. Щоб підкреслити таку особливість послідовного коливального контуру , говорять, що у послідовному коливальному контурі має місце резонанс напруги.

По аналогії, у паралельному коливальному контурі спостерігається резонанс струмів, бо струм у вітках з реактивними елементами на резонансній частоті у 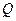разів перевищує вхідний струм .

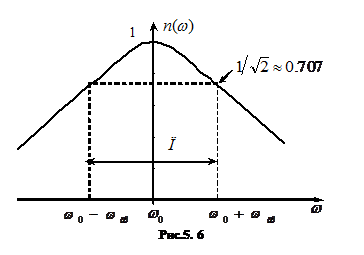Для оцінки вибірних властивостей контурів впроваджена така характеристика як смуга пропускання. Якісно вона визначається як ділянка частот , в межах якої гармонічні сигнали передаються без значних спотворень. Конкретизуючи вислів ’’без значних спотворень’’ отримують кількісну характеристику смуги пропускання. На практиці, в залежності від ситуаціїї, кількісні оцінки допустимих спотворень можуть змінюватися. Тому умовно для визначення смуги прозорості приймають деякий зручний, стандартний критерій допустимих спотворень., а саме - це ділянка частот, на краях якої резонансна характеристика (5.18) зменшується до рівня 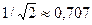(див.рис.5.6). Іншими словами, у смузі пропускання спотворення АЧХ не перевищують 3дБ. Такому критерію на краях смуги пропускання відповідає одиничне значення узагальненої розстройки - 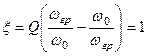. Звідки - 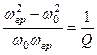, або

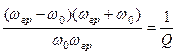. (5.23)

При значних добротностях - 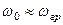, а 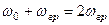. Враховуючи це із (5.23) отримаємо наближену формулу для визначення смуги пропускання :

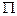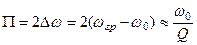. (5.24)

Скориставшись наближенням, ми свідомо внесли похибку у визначення смуги прозорості. Оціними відносне значення цієї похибки. Абсолютна похибка у визначенні смуги пропускання очевидно дорівнює:

.

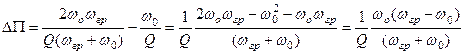Відносна похибка приведена до точного значення:

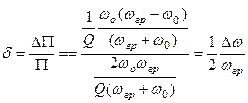. (5.25)