Частотні характеристики послідовного коливального контуру.

Реактивний опір контуру

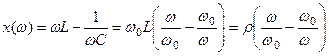. (5.5)

На резонансній частоті індуктивний опір контуру компенсує ємнісний опір, тому реактивний опір дорівнює нулеві і вхідний імпеданс визначається лише активним опором контуру. Як випливає з (5.5) на частотах 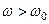- 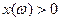, а це значить, що на частотах вищих за резонансну контур має індуктивний характер. На частотах 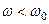- - 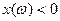коло буде мати ємнісний характер.

Якщо реактивний опір коливального контуру 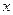дорівнює нулеві, то контур настроєний в резонанс з частотою зовнішньої ЕРС. Чим більше 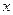відрізняється від нуля, тим більше розстроєний контур. В якості міри розстройки впроваджена безрозмірна величина, яку зазвичай позначають через і рівну відношенню реактивного опору контура до активного, це - узагальнена розстройка.

Вхідному імпедансу (5.1) можна надати і іншої форми

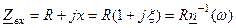, (5.6)

де 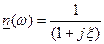, а 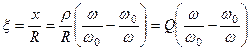- узагальнена розстройка контуру.

Повний опір

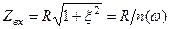, (5.7)

фазочастотна характеристика вхідного опору:

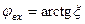. (5.8)

Вхідний струм:

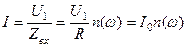, (5.9)

де 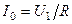- струм у контурі при резонансі.

Комплексна передаточна функція за напругою (вихідна напруга – напруга на конденсаторі, тобто ):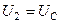

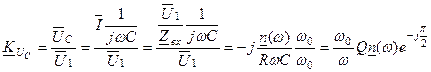. (5.10)

Якщо за вихідну напругу взяти напругу на індуктивній котушці, тобто 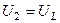, то -

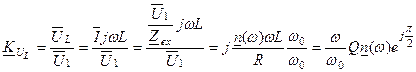. (5.11)

Отже частотні характеристики послідовного контуру в основному визначаються множником .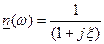

5.3.Паралельний коливальний контур.

Резонанс спостерігається також у колі з паралельно з’єднаними пасивними елементами 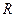, 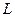та 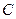(рис.5.3) - паралельному коливальному контурі. Вхідний імпеданс

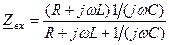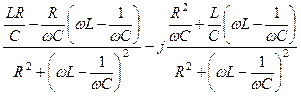= . (5.12)

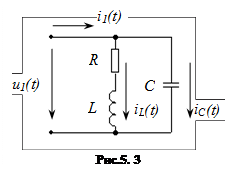Щоб струм співпадав за фазою з напругою, необхідно, щоб реактивна складова вхідного імпедансу дорівнювала нулеві. Тоді коло буде мати лише активний опір. Це еквівалентно дотримання рівності 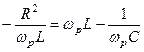. Звідки резонансна частота 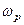паралельного коливального контуру –

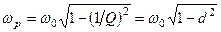. (5.13)

Отже резонансна частота паралельного коливального контуру дещо відрізняється від частоти власних коливань. Для контурів із значною добротністю ( ) - .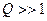

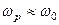На частотах близьких до резонансної 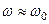та значних добротностях також виконуєтться нерівність 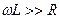. Тоді з урахуванням (5.12), (5.13) вхідний імпеданс

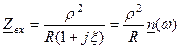. (5.14)

Знайдемо передаточну характеристику за струмом

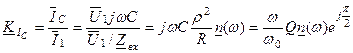. (5.15)

Якщо за вихідний вважати струм у вітці з індуктивною котушкою , то передаточна функція за струмом в даному випадку буде наступною:

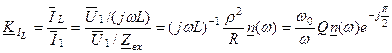. (5.16)

При незначному внутрішньому опорі джерела, очевидно, що передаточна функція за напругою буде дорівнювати :

.

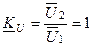Проте якщо живлення на контур подавати від джерела з внутрішнім опором значно більшим від вхідного опору контура на резонансній частоті 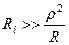, то очевидно

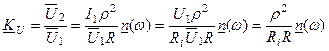(5.17)