Індуктивно-зв’язані коливальні контури.
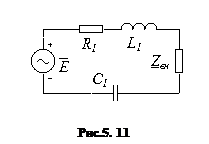
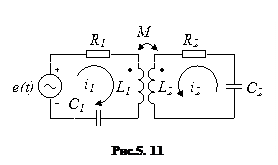 Розглянемо два індуктивно- зв’язані контури (рис.5.11). Вплив одного контуру на інший оцінюють коефіцієнтом зв’язку. Нехай в першому контурі тече змінний струм
Розглянемо два індуктивно- зв’язані контури (рис.5.11). Вплив одного контуру на інший оцінюють коефіцієнтом зв’язку. Нехай в першому контурі тече змінний струм 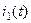 а другий розімкнутий. При проходжені струму
а другий розімкнутий. При проходжені струму 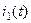 на затискачах котушки
на затискачах котушки 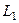 виникає е.р.с. самоіндукції
виникає е.р.с. самоіндукції 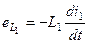 а на затискачах котушки
а на затискачах котушки 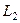 наводиться е.р.с взаємної індукції
наводиться е.р.с взаємної індукції 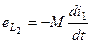 . Відношення цих е.р.с і є ступінь зв’язку
. Відношення цих е.р.с і є ступінь зв’язку 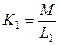 .
.
Якщо струм 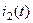 тече у вторинному контурі, то
тече у вторинному контурі, то 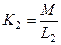 .
.
Коефіцієнтом зв’язку контурів називають геометричне середнє від 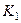 та
та 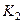 :
:
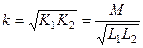 . (5.35)
. (5.35)
Розглянемо вимушені коливання у системі двух трансформаторно зв’язаних контурів (рис.5.11). За другим законом Кірхгофа складемо рівняння для первинного та вторинного контурів:
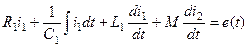 , (5.36)
, (5.36)
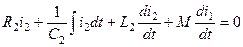 . (5.37)
. (5.37)
Нехай у первинному контурі діє джерело гармонічної е.р.с..Для знаходження струму у контурах скористаємося методом комплексних амплітуд, і перепишемо рівняння (5.36) та (5.37) у вигляді
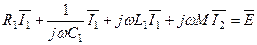 (5.38)
(5.38)
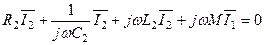 . (5.39)
. (5.39)
Позначимо власні імпеданси контурів через 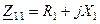 та
та 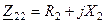 ( тут
( тут 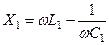 та
та 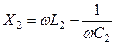 - реактивні опори контурів) , а через
- реактивні опори контурів) , а через 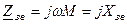 - опір зв’язку, і перепишемо рівняння (5.38),(5.39) у вигляді
- опір зв’язку, і перепишемо рівняння (5.38),(5.39) у вигляді
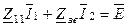 , (5.40)
, (5.40)
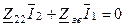 . (5.41)
. (5.41)
 Знайдемо
Знайдемо 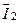 із другого рівняння (
із другого рівняння ( 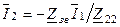 ) і підставимо у перше:
) і підставимо у перше:
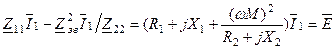 .
.
Позбудемося комплексності у знаменнику:
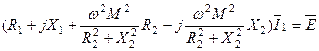 .
.
На основі останнього рівняння синтезуємо одноконтурне коло (рис.5.12) із еквівалентним комплексним опором
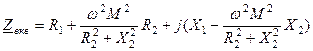 . (5.42)
. (5.42)
Таким чином систему двох зв’язаних контурів замінено еквівалентним послідовним коливальним контуром у якого:
1) еквівалентний активний опір -
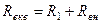 , де
, де 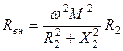 - внесений активний опір;
- внесений активний опір;
2) еквівалентний реактивний опір -
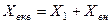 , де
, де 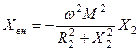 - внесений реактивний опір.
- внесений реактивний опір.
Дата добавления: 2015-08-14; просмотров: 1741;
