Настройка системи двох зв’язаних контурів.
Процес зміни параметрів контурів з метою отримання максимального значення струму у вторинному контурі називається настройкою. Очевидно, що настройку можна здійснювати, змінюючи параметри елементів (найчастіше змінюють ємність конденсаторів) контурів та зв’язку. В залежності від конструктивних особливостей контурів настройку можна здійснювати шляхом зміни параметрів лише первинного контуру, лише вторинного, одночасно первинного і вторинного і зв’язку. У відповідності з цим і виділяють наступні способи настройки контурів: перший та другий частинні резонанси, індивідуальний резонанс, складний та повний резонанси. При визначенні струму в залежності від способу настройки зручно користуватися наступним значенням струму у вторинному контурі, що випливає із рівнянь (5.40) та (5.41):
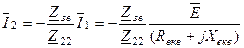 . (5.43)
. (5.43)
Замінимо алгебраїчну форму комплексних чисел у (5.43) показниковою: 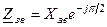 ,
, 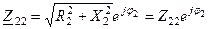 ,
, 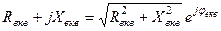 ,
, 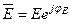 . Тоді
. Тоді
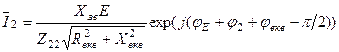 .
.
Отже модуль струму у вторинному контурі
 . (5.44)
. (5.44)
Перший частинний резонанс. Конструктивно система зв’язаних контурів побудована так, що існує доступ лише до елементів первинного контуру (на практиці до конденсатора). Змінюючи ємність конденсатора, можемо впливати на 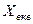 . Струм
. Струм 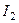 набуде максимального значення при
набуде максимального значення при 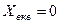 . Отже перший частинний резонанс має місце при
. Отже перший частинний резонанс має місце при
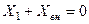 . (5.45)
. (5.45)
При цьому струм у вторинному контурі буде максимальним -
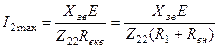 . (5.46)
. (5.46)
Другий частинний резонанс. Настройка способом другого частинного резонансу здійснюється шляхом зміни параметрів вторинного контуру (на практиці зміною ємності конденсатора ). Для визначення впливу на струм зручно користуватися наступним виразом
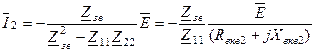 , (5.47)
, (5.47)
де 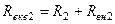 ,
, 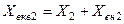 , а
, а 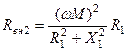 та
та  -внесені із первинного контуру у вторинний активний та реактивний опори відповідно. По аналогії з (5.43) перепишемо формулу (5.47)
-внесені із первинного контуру у вторинний активний та реактивний опори відповідно. По аналогії з (5.43) перепишемо формулу (5.47)
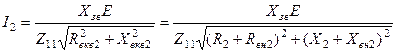 . (5.48)
. (5.48)
Отже у відповідності з формулою (5.48) струм у вторинному контурі при зміні 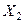 буде максимальним при
буде максимальним при
 . (5.49)
. (5.49)
Співвідношення (5.49) є необхідною умовою для настройки системи на другий частинний резонанс. Струм у вторинному контурі при настройці системи у другий частнний резонанс -
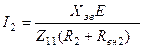
Індивідуальний резонанс. При такому способу настройки кожний контур окремо настроюють на частоту генератора. Спочатку настроюється первинний контур в резонанс по максимуму струму у вторинному контурі при слабому зв’язку. Потім здійснюється настройка другого контуру в резонанс теж при слабому зв’язку. Після виконання подібних операцій
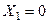 та
та 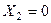 . (5.50)
. (5.50)
При дотриманні умов індивідуального резонансу (5.50) струм у вторинному контурі
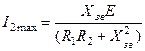 . (5.51)
. (5.51)
Складний резонанс. Конструктивні особливості системи двох зв’язаних контурів дозволяють змінювати параметри первинного контуру і втручатись у зв’язок. Спочатку систему настроюють у перший частинний резонанс. Потім змінюючи зв’язок добиваються максимального значення струму 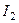 . Математично ’’настройка’’ на складний резонанс здійснюється шляхом дослідження на екстремум залежності (5.46) (змінною є зв’язок
. Математично ’’настройка’’ на складний резонанс здійснюється шляхом дослідження на екстремум залежності (5.46) (змінною є зв’язок 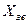 ). Для цього перепишемо (5.46) у формі:
). Для цього перепишемо (5.46) у формі:
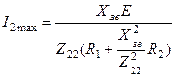 . (5.52)
. (5.52)
Похідна від (5.52) по 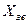 дорівнює нулеві при оптимальному зв’язку :
дорівнює нулеві при оптимальному зв’язку :
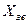 =
= 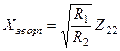 . (5.53)
. (5.53)
При складному резонансі струм у вторинному контурі досягає значення
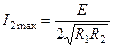 . (5.54)
. (5.54)
Повний резонанс. При повному резонансі систему спочатку настроюють у індивідуальний резонанс, а потім змінюючи зв’язок добиваються максимального значення струму 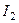 . При такому підході математичним об’єктом дослідження на екстремум є залежність (5.51) :
. При такому підході математичним об’єктом дослідження на екстремум є залежність (5.51) :
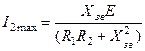 .
.
В даному випадку
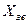 =
= 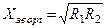 , (5.55)
, (5.55)
а максимальне значення струму буде таким як і при виконанні умови складного резонансу , тобто 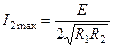 . Проте оптимальний коефіцієнт зв’язку при повному резонансі буде меншим від оптимального коефіцієнту зв’язку при складному резонансі (порівняйте значення (5.53) та (5.55)).
. Проте оптимальний коефіцієнт зв’язку при повному резонансі буде меншим від оптимального коефіцієнту зв’язку при складному резонансі (порівняйте значення (5.53) та (5.55)).
Оптимальний коефіцієнт зв’язку при повному резонансі називається критичним зв’язком. Знайдемо значення критичного коефіцієнту зв’язку:
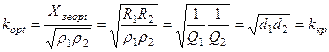 . (5.56)
. (5.56)
Якщо контури ідентичні, то
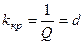 . (5.57)
. (5.57)
При 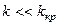 зв’язок прийнято називати слабким, а при
зв’язок прийнято називати слабким, а при 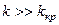 - сильним.
- сильним.
Дата добавления: 2015-08-14; просмотров: 1340;
