Енергетичні процеси у коливальних контурах.

Розглянемо енергетичні процеси на прикладі послідовного коливального контуру. Нехай на вхід контуру подається гармонічна напруга 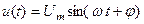. Тоді коло споживає струм 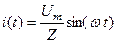, де - 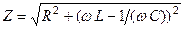повний опір кола, а .

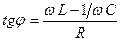Миттєве значення потужності, яку віддає джерело у даний двополюсник

.

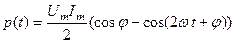Миттєві потужності, що споживаються елементами контуру:

; ; .

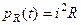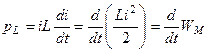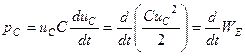Оскільки у колах змінного струму виконується баланс миттєвих потужностей то

.

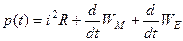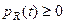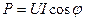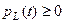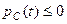Резистор у будь-яку мить часу споживає електромагнітну енергію, бо , причому максимум споживання спостерігається при екстремальних значеннях струму. Середнє за період значення потужності, яку споживає резистор - . Потужності, що споживаються індуктивною котушкою та конденсатором знакозмінні. І якщо то , бо напруга на конденсаторі знаходиться у квадратурі зі струмом індуктивної котушки. Тобто у колі відбувається обмін енергією між конденсатором та індуктивною котушкою. У відсутності резонансу циклічний обмін енергією не збалансований. Насправді, оскільки відношення максимальної енергії накопиченої у магнітному полі індуктивної котушки 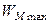до максимальної енергії накопиченої у електричному полі конденсатора 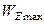є рівним

,

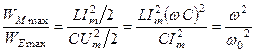то на частотах 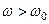коло буде мати індуктивний характер і . Надлишок енергії

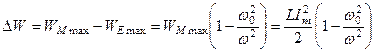(5.68)

коло повертає у джерело (частина енергії накопиченої у котушці витрачається на ’’підзарядку’’ джерела).

Переконаємося у цьому. Для спрощення викладок будемо вважати, що у колі відсутні активні втрати, тобто покладемо 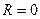. Тод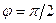і і 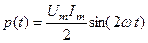. Отже 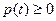при 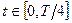, тобто на цій ділянці періоду гармонічеих коливань основної частоти 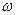джерело споживає енергію 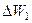. Знайдемо цю енергію

.

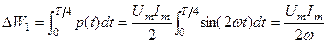Оскільки 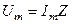, а 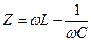, то остаточно

.

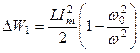Таким чином ми переконалися у тому, що при незбалансованому обміні енергією надлишок накопиченої енергії (5.68) у індуктивній котушці 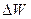у точності співпадає з енергією .

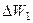Аналогічні процеси мають місце і на частотах .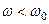

При резонансі ( 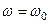отже - 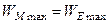і 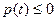) обмін енергією між реактивними елементами збалансований, і енергія джерела витрачається лише на компенсацію втрат на резисторі.

Знайдемо відношення максимальної накопиченої енергії до активних втрат за період у контурі на резонансній частоті

.

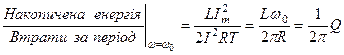З цієї формули випливає найбільш загальне означення добротності, яке пригодне як для механічних коливальних систем , так і для осциляторів у атомній фізиці -

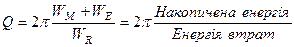. (5.69)