Частотні характеристики двох індуктивно зв’язаних контурів.
Розглянемо детально вхідний опір 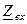 . Нехай обидва контури однакові, тобто
. Нехай обидва контури однакові, тобто 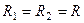 ,
, 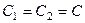 ,
, 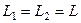 та
та 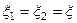 . Тоді на основі (5.42) при даних припущеннях
. Тоді на основі (5.42) при даних припущеннях
 . (5.58)
. (5.58)
Безрозмірну величину
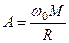 (5.59)
(5.59)
називають фактором зв’язку контурів. З іншої сторони , оскільки  , то фактор зв’язку дорівнює
, то фактор зв’язку дорівнює 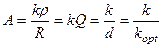 На частотах
На частотах 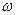 , близьких до резонансної
, близьких до резонансної 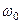 , вхідному імпедансу (5.58) можна надати наступну форму
, вхідному імпедансу (5.58) можна надати наступну форму
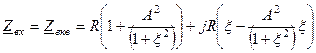 .
.
Звідси активна та реактивна складова вхідного імпедансу відповідно будуть
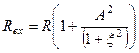 ; (5.60)
; (5.60)
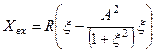 . (5.61)
. (5.61)
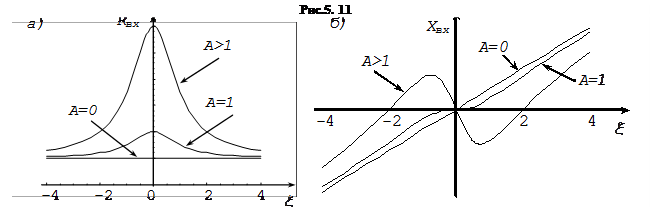 |
Активна складова вхідного опору (5.60) має два доданки: перший - вхідний опір послідовного коливального контуру на резонансній частоті, другий доданок
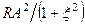 - внесений опір, з точністю до постійного множника співпадає із вхідним опором паралельного коливального контуру. Графік залежності
- внесений опір, з точністю до постійного множника співпадає із вхідним опором паралельного коливального контуру. Графік залежності 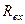 від узагальненої розстройки при різних факторах зв’язку показаний на рис.5.13,а.
від узагальненої розстройки при різних факторах зв’язку показаний на рис.5.13,а.
Реактивна частина вхідного опору (5.61) теж складається із двох доданків: перший доданок доданок 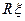 - реактивна складова вхідного опору послідовного коливального контуру , другий - внесений реактивний опір
- реактивна складова вхідного опору послідовного коливального контуру , другий - внесений реактивний опір 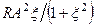 , постійним множником відрізняється від реактивного опору паралельного коливального контуру. Графік залежності
, постійним множником відрізняється від реактивного опору паралельного коливального контуру. Графік залежності 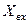 від узагальненої розстройки при різних факторах зв’язку показаний на рис.5.13,б.
від узагальненої розстройки при різних факторах зв’язку показаний на рис.5.13,б.
Отже, аналіз залежностей активної та реактивної складових вхідного вказує на те, що:
· при слабому зв’язку ( 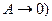
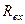 та
та 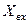 двох зв’язаних контурів співпадають з відповідними функціями послідовного коливального контуру;
двох зв’язаних контурів співпадають з відповідними функціями послідовного коливального контуру;
· при збільшені зв’язку між контурами 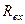 збільшуєтться;
збільшуєтться;
· залежість реактивного опору 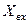 від фактора зв’язку
від фактора зв’язку  та узагальненої розстройки
та узагальненої розстройки  не проста. При
не проста. При 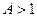 графік
графік 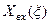 тричі перетинає вісь абсцис.
тричі перетинає вісь абсцис.
Резонанс у двох зв’язаних контурів має місце на частотах, при яких 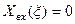 . Звідси з урахуванням (5.61) знаходимо узагальнені розстройки
. Звідси з урахуванням (5.61) знаходимо узагальнені розстройки 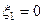 ,
, 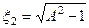 ,
, 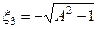 яким відповідають резонансні частоти:
яким відповідають резонансні частоти:
 ;
; 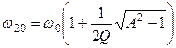 ;
;  . (5.62)
. (5.62)
Резонанс на частотах 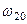 та
та 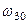 має місце лише при
має місце лише при 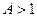 (або при
(або при  ) . Частоти
) . Частоти 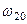 та
та 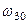 називаються частотами зв’язку . При
називаються частотами зв’язку . При 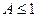 (
( 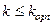 ) зв’язаним контурам притаманна лише одна резонансна частота
) зв’язаним контурам притаманна лише одна резонансна частота  . Зв’язок між контурами називається критичним зв’язком, якщо
. Зв’язок між контурами називається критичним зв’язком, якщо  (
( 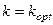 ) .
) .
Знайдемо значення комплексного коефіцієнта передачі за напругою 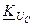 (за вихідну будемо вважати напругу на конденсаторі вторинного контуру). Із системи рівнянь (5.40, 5.41) комплексна амплітуда струму у вторинному контурі -
(за вихідну будемо вважати напругу на конденсаторі вторинного контуру). Із системи рівнянь (5.40, 5.41) комплексна амплітуда струму у вторинному контурі - 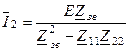 . Отже комплексна амплітуда напруги на конденсаторі -
. Отже комплексна амплітуда напруги на конденсаторі - 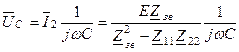 , а значення передаточної функції
, а значення передаточної функції 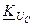 при умові, що контури ідентичні, буде наступним
при умові, що контури ідентичні, буде наступним
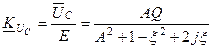 .
.
Модуль цієї функціїї -
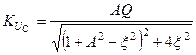 (5.63)
(5.63)
- АЧХ системи двої зв’язаних контурів , а аргумент
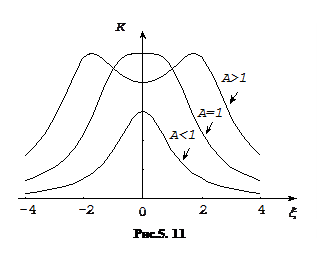
 (5.64)
(5.64)
-фазочастотна характеристика зв’язаних контурів.
На яких частотах АЧХ набуває екстремальних значень? На тих частотах що і підкореневий вираз у знаменнику (5.63). Елементарні дослідження на екстремум показують, що якщо фактор зв’язку 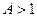 , то знаменник набуває екстремальних значень при розстройках , що відповідають фазовому резонансу зв’язаних контурів тобто частотам (5.62). Причому на частотах зв’язку
, то знаменник набуває екстремальних значень при розстройках , що відповідають фазовому резонансу зв’язаних контурів тобто частотам (5.62). Причому на частотах зв’язку 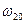 та
та 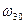 має місце максимум а на частоті
має місце максимум а на частоті 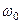 спостерігається мінімум у поведінці АЧХ , тобто АЧХ стає двухгорбовою.
спостерігається мінімум у поведінці АЧХ , тобто АЧХ стає двухгорбовою.
При 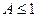 амплітудно-частотна характеристика - одноекстремальна. Екстремум спостерігається на частоті
амплітудно-частотна характеристика - одноекстремальна. Екстремум спостерігається на частоті 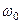 , тобто при нульовій узагальненій розстройці. АЧХ двох зв’язаних контурів при різних факторах зв’язку показані на рис.5.14. Форма цих кривих більш близька до прямокутної ніж у одиночного коливального контуру. У цьому легко переконатися якщо дослідити темп спаду АЧХ згаданих контурів за межами смуги пропускання (необхідно порівняти лише похідні )
, тобто при нульовій узагальненій розстройці. АЧХ двох зв’язаних контурів при різних факторах зв’язку показані на рис.5.14. Форма цих кривих більш близька до прямокутної ніж у одиночного коливального контуру. У цьому легко переконатися якщо дослідити темп спаду АЧХ згаданих контурів за межами смуги пропускання (необхідно порівняти лише похідні )
Знайдемо смугу пропускання двох зв’язаних контурів при різних зв’язках. При слабому зв’язку максимальне значення АЧХ при 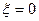 -
- 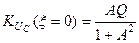 . На граничній частоті
. На граничній частоті 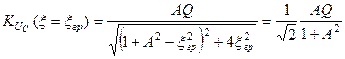 . Звідки при
. Звідки при 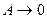 -
-  0,64, а смуга пропускання -
0,64, а смуга пропускання -
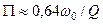 . (5.65)
. (5.65)
При критичному зв’язку (  ) -
) - 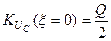 ,
, 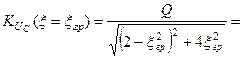 =
= 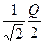 , а
, а 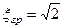 . Отже смуга пропускання у цьому випадку -
. Отже смуга пропускання у цьому випадку -
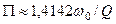 . (5.66)
. (5.66)
При сильному зв’язку ( 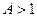 ) амплітудно-частотна характеристика зв’язаних контурів стає двухгорбовою. При розстройках, що відповідають частотам зв’язку
) амплітудно-частотна характеристика зв’язаних контурів стає двухгорбовою. При розстройках, що відповідають частотам зв’язку 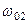 та
та 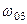 АЧХ набуває максимального значення -
АЧХ набуває максимального значення - 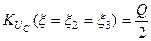 , а на частоті
, а на частоті  мінімального -
мінімального - 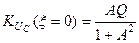 . Оскільки допустимі спотворення у смузі пропускання не повинні перевищувати 3дБ, то
. Оскільки допустимі спотворення у смузі пропускання не повинні перевищувати 3дБ, то 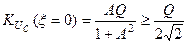 . Звідки знаходимо максимальне значення фактору зв’язку, яке задовільняє вказаному критерію допустимих спотворень -
. Звідки знаходимо максимальне значення фактору зв’язку, яке задовільняє вказаному критерію допустимих спотворень - 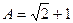 . При такому зв’язку смуга пропускання -
. При такому зв’язку смуга пропускання -
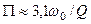 . (5.67)
. (5.67)
Таким чином змінюючи лише зв’язок у системі двох зв’язаних контурів можна регулювати смугу пропускання від мінімального значення (5.65) до максимального (5.67).
В радіоелектроніці використовуються і системи із більшої кількості зв’язаних контурів. Вони дістали назву фільтрів зосередженої селекції. АЧХ таких фільтрів ще у більшій мірі схожа на прямокутну.
Дата добавления: 2015-08-14; просмотров: 1620;
