Формула Мора для вычисления перемещения конструкции

Рассмотрим балку.

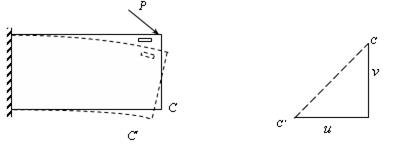
Под действием P, точка С перейдет 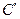, а каждый малый элемент деформируется.

Рассмотри задачу отыскания перемещения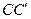

Чтобы найти 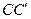, разложим его на вертикальную и горизонтальную составляющие.

Тогда: .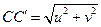

Введем обозначения: 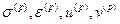- напряжения, деформации, перемещения, полученные при действии внешней силы Р .

Далее рассмотрим другую, фиктивную задачу для нашей конструкции, а именно, приложим единичную силу Т по вертикали в рассматриваемой точке С.

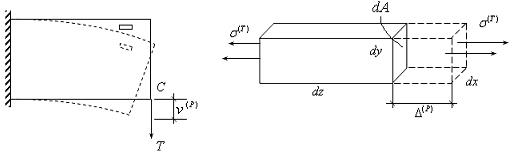
Здесь все малые элементы тоже получают деформации. Введем обозначения: 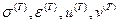- напряжения, деформации, перемещения, полученные при действии силы Т.

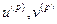Для вычисления в точке С применим закон сохранения энергии в варианте принципа возможных перемещений,. В качестве возможных выберем перемещения . Вычислим работу силы Т на возможном перемещении :

.

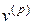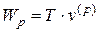Эта работа согласно закону сохранения должна быть равна работе 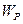по преодолению сил сопротивления (напряжений 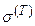), требуемых для деформирования малых элементов на величину 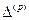(возможную абсолютную деформацию малого элемента). Подсчитаем ее.

Рассмотрим малый элемент. Сила его растяжения - будет:

.

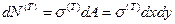Согласно определению относительное удлинение от силы Р – это линейная деформация 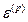, следовательно, удлинение нашего малого элемента будет:

.

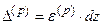Подсчитываем работу, которую совершает сила 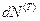на перемещение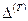

.

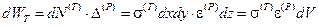Во всем теле суммарная работа будет:

.

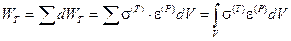Запишем закон сохранения энергии: W_Т=W_Р.

Отсюда: .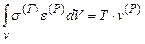

Для удобства счета принимают Т=1, тогда формула Мора примет вид:

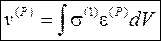
- искомое перемещение

- деформация, которую вызывают внешние силы Р

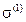- напряжение, которое создано единичной силой Т

Т – единичная сила, которая приложена в интересующей нас точке и в интересующем нас направлении.

Примечание. Если после вычисления получится что , то это значит, что направление перемещения нужно выбрать в другую сторону, т.е. она направлено против направления действия силы Т=1.