Главные напряжения
Рассмотрим общий случай воздействия на элемент тела напряжений 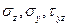 .
.
Для этого сложим все 3 формулы и получим :
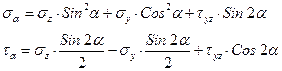
Эти формулы подобны формулам для осевых и центробежных моментов инерции для повернутых осей. Поэтому аналогично вводятся и понятия главных напряжений и главных площадок. Если вычислить 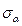 для разных углов, то можно найти максимальное и минимальное
для разных углов, то можно найти максимальное и минимальное 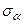 . Эти напряжения называются главными.
. Эти напряжения называются главными.
Обозначается:
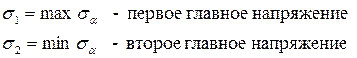
Главные площадки – это сечения, на которых 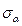 экстремальны.
экстремальны.
Угол 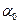 , который определяет положение главных площадок, получаем по теореме Ферма: при
, который определяет положение главных площадок, получаем по теореме Ферма: при 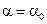 должно быть
должно быть 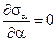
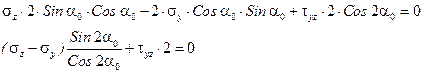
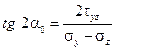
Отсюда находим 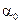 .
.
Аналогично теории геометрических характеристик можно видеть, что на этих новых площадках касательных напряжений не будет, т.е.
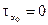 .
.
Следствие:
Всегда можно найти в теле такое положение малого элемента, в котором он только растягивается или сжимается, причем эти напряжения будут экстремальными.
Примечание: согласно свойствам 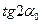 , если взять угол
, если взять угол 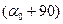 , то условие
, то условие 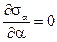 снова удовлетворится. Таким образом, существуют 2 главные площадки под углами
снова удовлетворится. Таким образом, существуют 2 главные площадки под углами 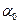 и
и 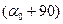 .
.
Вычисление 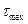
В некотором теле найдем главные площадки для малого элемента.

Рис.11.7 Рис.11.8
Оси, ортогональные главным площадкам, обозначим 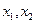 . На главных площадках
. На главных площадках 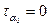
Рассмотрим площадку под углом 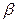 . Используя формулу для
. Используя формулу для 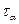 при
при 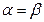 получим:
получим: 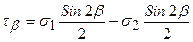

Поскольку 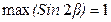 , то
, то 
Таким образом, 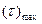 возникает на площадках, расположенных под углом
возникает на площадках, расположенных под углом 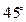 к главной площадке
к главной площадке
Можно показать, что в случае, когда действуют лишь напряжения 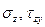 значения главных напряжений можно вычислять даже не зная положения главных площадок по формулам :
значения главных напряжений можно вычислять даже не зная положения главных площадок по формулам :

Тогда: 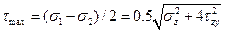 .
.
Дата добавления: 2015-08-11; просмотров: 675;
