Вторая теория прочности
Утверждается, что разрушение элемента наступает тогда, когда максимальная деформация удлинения 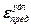 достигает предельного значения
достигает предельного значения 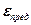 , то есть или при:
, то есть или при:

или же при
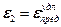 .
.
В компонентах 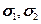 это условие записывается с помощью закона Гука:
это условие записывается с помощью закона Гука:
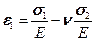 ,
, 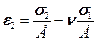 .
.
Тогда получим:
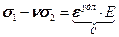 .
.
Выразим С через  . Для этого учтем, что это условие должно быть справедливо и при разрушении простым растяжением. Тогда:
. Для этого учтем, что это условие должно быть справедливо и при разрушении простым растяжением. Тогда:
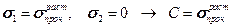
Таким образом, вторая теория примет вид:

 или
или
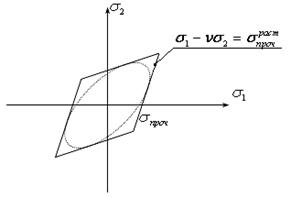
Рис.11.14
Аналогичные соотношения получим при деформации укорочения:

 или
или
Предельная поверхность примет вид, изображенный на рисунке 11.14 в виде многоугольника. Вторая теория плохо коррелирует с экспериментом.
11.5.3.Третья теория прочности (теория максимальных касательных напряжений)
Эта теория удовлетворительно согласуется с экспериментами над материалами, у которых пределы прочности на растяжение и сжатие одинаковы (например, для стали).
Согласно III теории, утверждается, что разрушение наступит тогда, когда в каком-то элементе 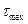 достигнет предельного значения, то есть при:
достигнет предельного значения, то есть при:
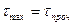 .
.
Как было получено ранее, максимальные касательные напряжения 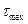 возникают на площадках, наклоненных под углом 45о к направлению действия
возникают на площадках, наклоненных под углом 45о к направлению действия 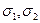 , и определяются по формуле:
, и определяются по формуле:
 .
.
Выразим 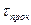 через
через  . Условие прочности должно быть справедливо и при разрушении простым растяжением, т.е. тогда, когда:
. Условие прочности должно быть справедливо и при разрушении простым растяжением, т.е. тогда, когда:

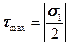 .
.
Из условия прочности 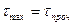 вытекает, что:
вытекает, что:
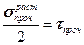 .
.
Аналогичные максимальные касательные напряжения 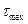 возникают на площадках, наклоненных под углом 45о к направлению действия
возникают на площадках, наклоненных под углом 45о к направлению действия  , и
, и 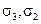 . Они определяются по формулам
. Они определяются по формулам
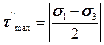 ,
, 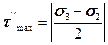 .
.
Таким образом, окончательно условие потери прочности примет вид:
или 
или 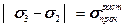
или 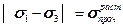
В строительстве при расчете балок, плит перекрытия, балок стенок считается, что большие напряжения возникаю только в одной плоскости, т.е. 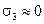 . Тогда из
. Тогда из 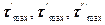 напряжение
напряжение 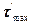 будет наибольшим только тогда, когда
будет наибольшим только тогда, когда 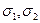 имеют различные знаки, т.е. во 2-ой и 4-ой квадрантах. Если же
имеют различные знаки, т.е. во 2-ой и 4-ой квадрантах. Если же 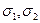 имеют одинаковые знаки (в первой и третьей квадрантах), то получим, что
имеют одинаковые знаки (в первой и третьей квадрантах), то получим, что 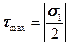 или
или 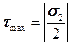 . Подставляя в условие прочности
. Подставляя в условие прочности 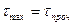 , получим
, получим
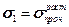 или или 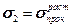 Таким образом, в первой и третьей квадрантах третья теория прочности совпадает с первой.
Предельная кривая в частном случае, когда
Таким образом, в первой и третьей квадрантах третья теория прочности совпадает с первой.
Предельная кривая в частном случае, когда  =0, примет вид шестиугольника, приведенного на рис.11.15. =0, примет вид шестиугольника, приведенного на рис.11.15.
| 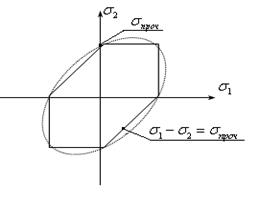 Рис.11.15
Рис.11.15
|
Дата добавления: 2015-08-11; просмотров: 773;
