Четвертая теория (энергетическая)
Она наилучшим образом согласуется с экспериментальными данными для пластичных материалов типа сталь. Утверждается, что элемент тела единичного объема разрушится тогда, когда работа максимальных касательных напряжений достигнет предельного значения.
Для трехосного напряженного состояния в разных плоскостях имеем 3 разных 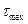 :
:
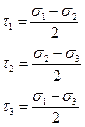
Рассмотрим работу 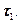

Рис.11.16
Имеем:
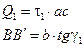
Работа силы 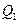 на перемещении
на перемещении  будет:
будет:
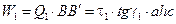 .
.
В виду малости угла сдвига имеем:
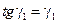 .
.
Примем, что объем элемента 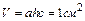
Таким образом, получаем:
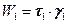 .
.
По закону Гука ( 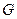 - модуль сдвига):
- модуль сдвига):
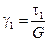 .
.
Окончательно получим: 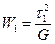 .
.
Аналогично, максимальные касательные напряжения в других плоскостях дают работы:
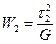 ,
, 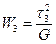 .
.
Суммируя их, получим:
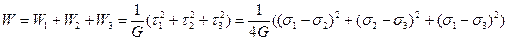 .
.
Обозначим работу внутренних сил, приводящих к разрушению элемента тела, через 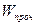 .
.
Тогда критерий разрушения можно записать в виде:
 .
.
Выразим правую часть через  . Рассмотрим частный случай - одноосное растяжение. Тогда в момент разрушения:
. Рассмотрим частный случай - одноосное растяжение. Тогда в момент разрушения:
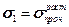
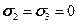 .
.
Подставляя в критерий разрушения, получим:
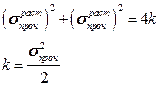
Окончательно четвертая теория теперь примет вид:
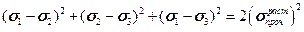 .
.
Рассмотрим теперь частный случай, когда  = 0, который имеет место в балках и плитах строительных сооружений. Тогда получим критерий в виде:
= 0, который имеет место в балках и плитах строительных сооружений. Тогда получим критерий в виде:
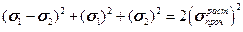 .
.
 или
или
Предельная кривая примет вид эллипса, приведенного на рис.11.15.
11.5.5. Пятая теория – критерий Мора
Формулируется для элемента тела, который растягивается в продольном направлении и сжимается в поперечном направлении (см. рис.11.18).
 | |||
 |
Рис.11.18. Рис.11.19.
Для некоторых материалов (например, для бетона) было обнаружено, что он, предварительно сжатый в поперечном направлении (см. рис.11.19), хуже работает на растяжение в продольном направлении.
Запишем это утверждение аналитически. Учтем, что при растяжении 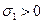 , при поперечном сжатии
, при поперечном сжатии 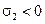 . Тогда разрушение произойдет при
. Тогда разрушение произойдет при
 ,
,
где n > 0 – некоторый коэффициент. Выразим n через пределы прочности материала.
 Для этого сначала рассмотрим разрушение при простом сжатии. Тогда получим:
Для этого сначала рассмотрим разрушение при простом сжатии. Тогда получим:
Отсюда:  .
.
Таким образом, для элемента тела, который растягивается в продольном направлении и сжимается в поперечном направлении получим критерий Мора в виде:
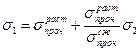 .
.
В 1-ой и 3-ей четвертях (т.е. при растяжении или сжатии в обоих направлениях) применяют первую теорию. Предельная кривая примет вид многоугольника, приведенный на рис.11.20.

Рис.11.20
Примечание. Если на элемент тела кроме 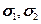 действует еще
действует еще 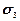 , при этом
, при этом 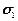
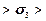
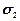 , а также
, а также  ,
,  , то критерий Мора записывают так же
, то критерий Мора записывают так же
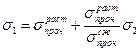 .
.
Это означает, что влиянием 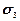 на прочность элемента пренебрегают.
на прочность элемента пренебрегают.
Дата добавления: 2015-08-11; просмотров: 821;
