Расчет цилиндрической оболочки под воздействием внутреннего давления

Рассмотрим применение теории прочности при расчете цилиндрической оболочки.

Рис 13.1	Рис 13.2	Рис 13.3

Пусть известны средний радиус оболочки R (в силу тонкостенности оболочки обычно работают со средним радиусом R),толщина стенки h, давление р внутри трубы.

В отличие от простого растяжения элементы стенки испытывают и продольное, и окружное растяжение.

Вырежем диск ширины b (pис. 13.1). На него действует давление р. Рассечем диск на 2 части. Нижняя часть воздействует на верхнюю давлением р и растягивает стенки трубы усилием N (pис. 13.3).

Из уравнений равновесия вытекает:

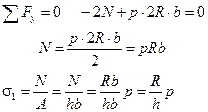
Рассмотрим второе сечение (pис 12.4).

Рис 13.4

На него слева действует давление p и сила N₂. Уравнение равновесия примет вид:

Отсюда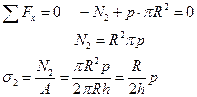

Видно, что окружные напряжения в два раза больше чем продольные. Согласно I,III и V теориям прочности при наличии растягивающих напряжений условия того, что разрушения не произойдет, имеют вид:

Или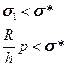

Отсюда находим давление, которое может выдержать цилиндрическая оболочка:

.

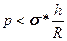Рассмотрим теперь IV теорию. Получим давление, которое может выдержать материал оболочки согласно этой теории:

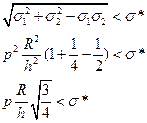
Видно, что IV теория даёт предельное давление, которое может выдержать оболочка, в 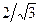раза большее, чем то давление, которое дают I,III и V теории. Таким образом, IV теория позволяет экономить материал приблизительно на 15%.