Условие независимости напряжений от времени в конструкциях из вязкоупругих материалов
Отметим следующий интересный факт. Оказывается, если материалы, из которых изготовлены конструкции, обладают линейно-вязко-упругими свойствами, причем они имеют коэффициенты вязкости, пропорциональные жесткостям этих материалов, то напряжения в конструкции не изменятся с течением времени (то есть релаксации не происходит, а происходит только деформация конструкции).
Проверим это на примере железобетонной колонны.
Примем, как и ранее:
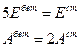
| 
|
Сделаем сечение. На него сверху действуют силы 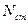 и
и 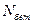
Согласно правила знаков:
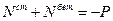 (9.6.2.1)
(9.6.2.1)

Условие совместности деформации:
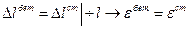
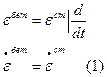
Полная деформация 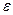 состоит из упругой части и деформации ползучести:
состоит из упругой части и деформации ползучести:
 =
= 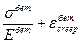

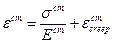
Возьмем производную по времени:
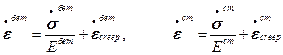
Согласно закону ползучести имеем:
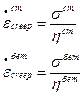

Таким образом: 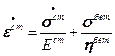
Подставим в (1) и получим:
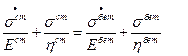 (9.6.2.2)
(9.6.2.2)
Выразим напряжения через силу P.
Из уравнения равновесия:
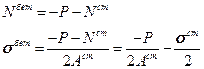
Подставим в (9.6.2.2). Учитывая, что 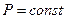 получим:
получим:
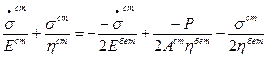 (9.6.2.3)
(9.6.2.3)
Запишем начальные условия для 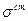 .
.
При t=0 деформаций ползучести еще нет 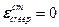 , то есть задача чисто упругая, следовательно, из предыдущих лекций можно записать решение:
, то есть задача чисто упругая, следовательно, из предыдущих лекций можно записать решение:
t=0: 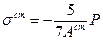 (9.6.2.4.)
(9.6.2.4.)
В теории линейных уравнений существует теорема: если найдено решение уравнения, которое удовлетворяет всем начальным условиям, то оно единственное.
Проверим, не является ли 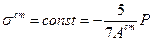 решением нашего уравнения (9.6.2.3). Подставим
решением нашего уравнения (9.6.2.3). Подставим 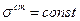 в (9.6.2.3.) и получим, что:
в (9.6.2.3.) и получим, что:
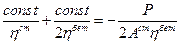 (9.6.2.5)
(9.6.2.5)
Примем, как говорилось выше, что вязкость стали, так же как и модуль упругости, в 5 раз больше вязкости бетона:
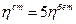 /
/
Подставляя в (9.6.2.5) получим
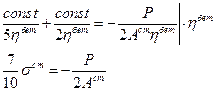
Подставив сюда 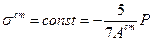 , получаем тождество
, получаем тождество

Это говорит о том, что 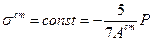 является решением дифференциального уравнения, следовательно, оно единственное. Таким образом, в арматуре напряжение не изменится со временем, следовательно, и в бетоне не будет релаксации (это следует из. (9.6.2.1)).
является решением дифференциального уравнения, следовательно, оно единственное. Таким образом, в арматуре напряжение не изменится со временем, следовательно, и в бетоне не будет релаксации (это следует из. (9.6.2.1)).
Что и требовалось показать.
Дата добавления: 2015-08-11; просмотров: 651;
