ОСНОВЫ ТЕОРИИ КОЛЕБАНИЙ

Развитие современной техники ставит перед инженерами самые разнообразные задачи, связанные с расчетом различных сооружений, с проектированием, производством и эксплуатацией всевозможных машин и механизмов.

Исследование поведения любой механической системы всегда начинается с выбора физической модели. Переходя от реальной системы к ее физической модели обычно упрощают систему, пренебрегая несущественными для данной задачи факторами. Так, исследуя систему, состоящую из груза, подвешенного на нити, пренебрегают размерами груза, массой и податливостью нити, сопротивлением среды, трением в точке подвеса и т.д.; при этом получается известная физическая модель — математический маятник.

Ограниченность физических моделей играет существенную роль при исследовании колебательных явлений в механических системах.

Физические модели, которые описываются системами линейных дифференциальных уравнений с постоянными коэффициентами принято называть линейными.

Выделение линейных моделей в особый класс вызывается рядом причин:

· С помощью линейных моделей исследуется широкий круг явлений, происходящих в различных механических системах;

· Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами является, с математической точки зрения, элементарной задачей и поэтому инженер–исследователь стремится по возможности описать поведение системы с помощью линейной модели.

Основные понятия и определения

Колебания системы считаются малыми, если отклонения и скорости можно рассматривать как величины первого порядка малости по сравнению с характерными размерами и скоростями точек системы.

Механическая система может совершать малые колебания только вблизи устойчивого положения равновесия. Равновесие системы может быть устойчивым, неустойчивым и безразличным (рис. 3. 8).

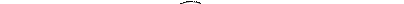
Рис. 3. 8 Различные виды равновесия

Равновесное положение системы является устойчивым, если система, равновесие которой нарушено весьма малым начальным отклонением 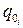и (или) малой начальной скоростью 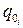, совершает движение около этого положения.

Критерий устойчивости положения равновесия консервативных систем с голономными и стационарными связями устанавливается по виду зависимости потенциальной энергии системы от обобщённых координат. Для консервативной системы c 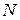степенями свободы, уравнения равновесия имеют вид

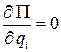, т.е. , где .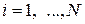

Сами уравнения равновесия не дают возможности оценить характер устойчивости или неустойчивости положения равновесия. Из них лишь следует, что положению равновесия соответствует экстремальное значение потенциальной энергии.

Условие устойчивости положения равновесия (достаточное) устанавливается теоремой Лагранжа – Дирихле:

если в положении равновесия системы потенциальная энергия имеет минимум, то это положение устойчиво.

Условием минимума любой функции является положительность второй производной от неё, при равенстве первой производной нулю. Поэтому

.

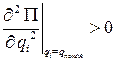Если же вторая производная тоже равна нулю, то для оценки устойчивости необходимо вычислить последовательные производные

,

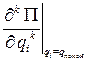и если первая не равная нулю производная имеет чётный порядок и при этом положительна, то потенциальная энергия при 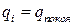имеет минимум, а следовательно, это положение равновесия системы устойчиво. Если же эта производная имеет нечётный порядок, то при 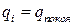нет ни максимума, ни минимума. Оценка состояния равновесия системы в положении, когда она не имеет минимума потенциальной энергии, приводится в специальных теоремах А. М. Ляпунова.