Потенциальная энергия системы
Потенциальная энергия системы с 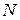 степенями свободы в общем случае является функцией обобщённых координат
степенями свободы в общем случае является функцией обобщённых координат
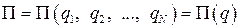 .
.
Рассмотрим только малые смещения системы из положения равновесия. В этом случае обобщённые координаты 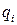 , отсчитываемые от равновесного положения, можно рассматривать как величины первого порядка малости.
, отсчитываемые от равновесного положения, можно рассматривать как величины первого порядка малости.
В положении равновесия системы 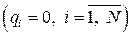 потенциальную энергию можно принять равной нулю
потенциальную энергию можно принять равной нулю 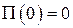 . Удерживая в разложении потенциальной энергии
. Удерживая в разложении потенциальной энергии 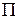 в ряд Маклорена только члены второго порядка малости, получаем
в ряд Маклорена только члены второго порядка малости, получаем
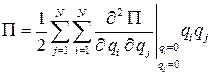 .
.
Обозначим
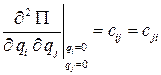 ,
, 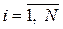 ;
; 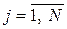 ,
,
где постоянные 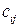 имеют название коэффициентов жёсткости. Таким образом, приближённое выражение для потенциальной энергии системы окончательно принимает вид квадратичной функции от обобщенных координат
имеют название коэффициентов жёсткости. Таким образом, приближённое выражение для потенциальной энергии системы окончательно принимает вид квадратичной функции от обобщенных координат 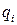 :
:
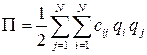 .
.
Для систем с одной степенью свободы потенциальная энергия вычисляется, следовательно, по формуле:
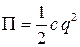 .
.
Дата добавления: 2015-08-08; просмотров: 768;
