Диссипативная функция Рэлея
Пусть на любую точку системы, имеющую 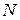 степеней свободы, действует сила сопротивления пропорциональная первой степени скорости
степеней свободы, действует сила сопротивления пропорциональная первой степени скорости
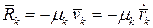 ,
,
где 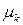 — коэффициент сопротивления.
— коэффициент сопротивления.
Силе сопротивления 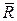 сопоставляется диссипативная функция Рэлея
сопоставляется диссипативная функция Рэлея 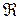 , характеризующая быстроту рассеивания (диссипации) энергии системы
, характеризующая быстроту рассеивания (диссипации) энергии системы
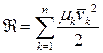 ,
,
которую при стационарных связях 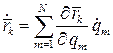 можно представить следующим образом:
можно представить следующим образом:
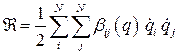 ,
,
где 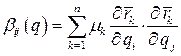 .
.
Для системы с конечным числом степеней свободы, ограничиваясь в разложении коэффициентов в ряд Маклорена только первыми членами, получим выражение функции рассеивания Рэлея в виде однородной положительной квадратичной функции обобщённых скоростей
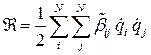 ,
,
где  — постоянные, называемые коэффициентами диссипации или приведёнными коэффициентами сопротивления.
— постоянные, называемые коэффициентами диссипации или приведёнными коэффициентами сопротивления.
Отсюда для системы с одной степенью свободы
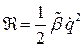 .
.
Дата добавления: 2015-08-08; просмотров: 2846;
