Затухающие колебания системы
Если на любую точку механической системы с наложенными стационарными голономными связями, кроме упругой силы, действует сила сопротивления пропорциональная первой степени скорости 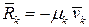 , то уравнение Лагранжа II рода можно записать в виде
, то уравнение Лагранжа II рода можно записать в виде
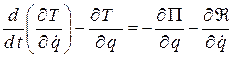 .
.
Подставляя выражения для кинетической, потенциальной энергии и диссипативной функции в уравнение Лагранжа II рода, получим
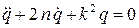
где 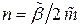 — коэффициент демпфирования (затухания).
— коэффициент демпфирования (затухания).
Т.к. корни характеристического уравнения соответствующие данному дифференциальному уравнению определяются выражениями
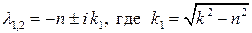 ,
,
то его решение зависит от соотношений между коэффициентами 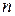 и
и 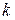 :
:
Ошибка! Закладка не определена. 
Рис. 3. 10 Апериодическое движение при большом сопротивлении
· 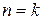 — решение имеет вид (рис. 3. 10):
— решение имеет вид (рис. 3. 10):
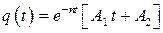 ;
;
· 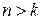 — решение имеет вид (рис. 3. 10):
— решение имеет вид (рис. 3. 10):
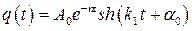 ,
,
где 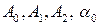 — также как и в случае колебательного движения без сопротивления, константы интегрирования, определяемые из начальных условий.
— также как и в случае колебательного движения без сопротивления, константы интегрирования, определяемые из начальных условий.
При 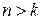 движение механической системы имеет апериодический характер, типичный график которого, изображен на рис. 3. 10.
движение механической системы имеет апериодический характер, типичный график которого, изображен на рис. 3. 10.
· 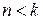 — (случай малого сопротивления) решение имеет вид (рис. 3. 11):
— (случай малого сопротивления) решение имеет вид (рис. 3. 11):
 или
или 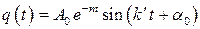 .
.
Здесь 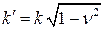 — называется частотой свободных затухающих колебаний,
— называется частотой свободных затухающих колебаний, 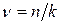 — относительный коэффициент затухания, константы интегрирования
— относительный коэффициент затухания, константы интегрирования 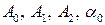 определяются из начальных условий
определяются из начальных условий 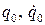 :
:
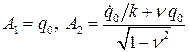 ,
, 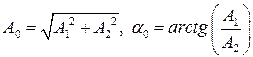 .
.
Величина 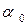 — как и в случае колебаний без учета сопротивления, называется начальной фазой колебаний. Коэффициент
— как и в случае колебаний без учета сопротивления, называется начальной фазой колебаний. Коэффициент 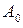 определяет координату пересечения образующей графика
определяет координату пересечения образующей графика 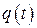 —
— 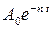 с осью
с осью 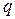 .(см. Рис. 3. 11)
.(см. Рис. 3. 11)
Ошибка! Закладка не определена. 
Рис. 3. 11 Свободные затухающие колебания.
Период затухающих колебаний определяется соотношением
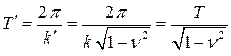 .
.
Степень затухания колебательного движения определяется декрементом колебаний 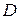 , который определяется отношением двух последовательных максимумов кривой
, который определяется отношением двух последовательных максимумов кривой 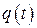 или логарифмическим декрементом
или логарифмическим декрементом 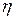 :
:
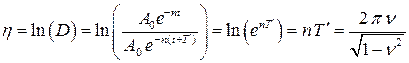 .
.
Дата добавления: 2015-08-08; просмотров: 704;
