Биения.

При частоте возмущающей силы, близкой к частоте свободных колебаний, наступает явление, называемое биениями.

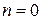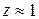Особенно ярко это явление проявляется при отсутствии сопротивления движению (см. рис. 3. 17), т. е. при и . В этом случае получим

,

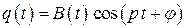где .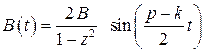

Ошибка! Закладка не определена.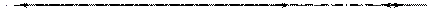

Рис. 3. 17 Биения при отсутствие сопротивления.

Ошибка! Закладка не определена.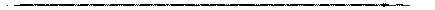

Рис. 3. 18 Биения при наличии сопротивления.

Движение, определяемые данным уравнением, можно рассматривать как колебания частоты 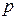и периода 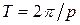, амплитуда которых 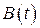является периодической функцией с периодом 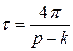. Так как 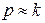, то период 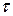велик по сравнению с периодом вынужденных колебаний .

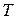Аналогичное явление можно получить и при наличии сопротивления движению (см. рис. 3. 18), в том случае, если коэффициент сопротивления 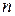достаточно мал.