Свободные колебания системы
Рассмотрим движение голономной механической системы с одной степенью свободы под действием упругой силы 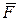 , обладающей потенциалом. Положение системы определяется одной обобщённой координатой
, обладающей потенциалом. Положение системы определяется одной обобщённой координатой 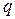 , которую будем отсчитывать от равновесного состояния. Тогда движение системы будет описываться одним уравнением Лагранжа II рода:
, которую будем отсчитывать от равновесного состояния. Тогда движение системы будет описываться одним уравнением Лагранжа II рода:
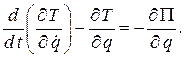
Подставляя значения кинетической и потенциальной энергии в уравнение Лагранжа, получим дифференциальное уравнение свободных колебаний системы.
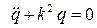 ,
,
где 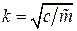 — частота свободных колебаний механической системы.
— частота свободных колебаний механической системы.
Решение этого уравнения можно записать в виде
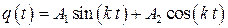 или
или 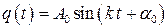 ,
,
где 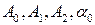 — константы, определяемые из начальных условий:
— константы, определяемые из начальных условий:
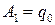 ,
, 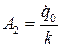 или
или  ,
, 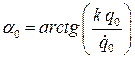 .
.
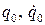 — начальное положение и начальная скорость.
— начальное положение и начальная скорость.
Типичный график движения механической системы, определяемый данным уравнением, изображен на рис. 3. 9. Коэффициенты интегрирования 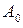 ,
, 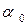 имеют вполне определенный механический смысл (см. рис. 3. 9):
имеют вполне определенный механический смысл (см. рис. 3. 9):
· 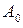 — амплитуда свободных колебаний,
— амплитуда свободных колебаний,
· 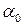 — начальнаяфаза колебаний.
— начальнаяфаза колебаний.
Ошибка! Закладка не определена. 
Рис. 3. 9 График свободных колебаний без учета сопротивления
Величина обратная частоте свободных колебаний называется периодом колебаний и определяется выражением 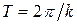 .
.
Дата добавления: 2015-08-08; просмотров: 638;
