Сферическое движение твердого тела

Твердое тело с одной неподвижной точкой имеет три степени свободы. Классическими параметрами, определяющими положение этого тела в пространстве, являются три угла Эйлера: 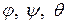. Если 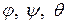известны как функции времени, то известно и движение твердого тела с одной неподвижной точкой (сферическое движение) (рис. 3.6).

Для составления дифференциальных уравнений сферического движения запишем теорему об изменении кинетического момента в дифференциальной форме

,

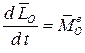где 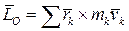— кинетический момент твердого тела, совершающего сферическое движение относительно неподвижной точки ;

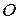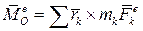— главный момент внешних сил относительно неподвижного центра .

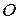Чтобы записать соответствующие формулы в наиболее простом виде возьмем в качестве координатных – подвижные главные оси инерции 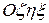жестко связанные с телом. Тогда проекции кинетического момента на оси координат можно записать в виде

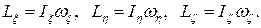
Уравнения движения (динамические уравнения Эйлера) в этом случае примут вид:

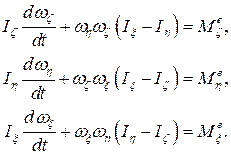
где 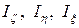– моменты инерции тела относительно его осей инерции в точке О;

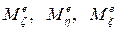– главные моменты внешних сил, приложенных к телу, относительно этих же осей.

К динамическим уравнениям Эйлера следует присоединить кинематические уравнения Эйлера:

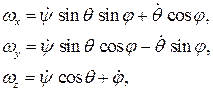
которые выражают проекции вектора угловой скорости вращения твердого тела на оси подвижной системы координат, скрепленные с телом через углы Эйлера и их производные по времени.

Рис. 3. 6 Сферическое движение твердого тела.

Динамические и кинематические уравнения Эйлера образуют систему шести нелинейных дифференциальных уравнений первого порядка; интегрирование этой системы представляет сложную математическую задачу. Для интегрирования этих уравнений при решении конкретных задач обычно используют те или иные приближенные математические методы.