Нахождение реакций в подшипниках

Дифференциальное уравнение вращательного движения не позволяет определить реакции опор, удерживающих тело на оси вращения. Для их нахождения необходимо применить теорему о движении центра масс и теорему об изменении кинетического момента, записанных в проекциях на оси координат или воспользоваться принципом Даламбера. Например, для декартовой системы координат 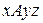(рис. 3. 5) получим

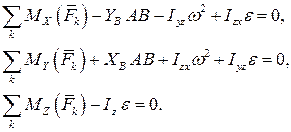
Последнее уравнение данной системы полностью совпадает с дифференциальным уравнением вращательного движения, полученного ранее.

Рис. 3. 5 Динамические реакции подшипников.

Для нахождения неизвестных реакций в подшипниках остается пять алгебраических уравнений. Обычно полные реакции в подшипниках раскладывают на статические и динамические составляющие

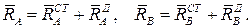
Статическими реакциями 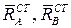называют части полных реакций, которые статически уравновешивают приложенные внешние силы. Уравнения для их определения получают из первых пяти уравнений, положив в них 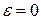и .

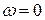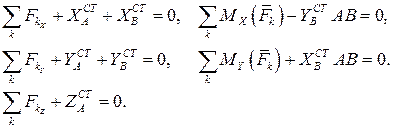
Части полных реакций 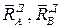, которые возникают при движении твердого тела, называют динамическими реакциями. Уравнения для их определения получаем с учетом того, что приложенные внешние силы уравновешиваются статическими реакциями

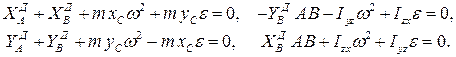
Когда центр масс твердого тела расположен на оси вращения, твердое тело называют статически уравновешенным. Динамические реакции в этом случае образуют пару сил.

Когда ось вращения является главной центральной осью инерции 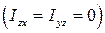и центр масс расположен на ней, имеем случай динамической уравновешенности. Динамические реакции равны нулю и в подшипниках возникают только статические реакции.