Вращательное движение вокруг неподвижной оси

Рассмотрим твёрдое тело, вращающееся вокруг неподвижной оси 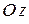. Угловую скорость его вращения в произвольный момент времени обозначим 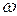. Тогда кинетический момент этого тела относительно оси 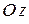равен

.

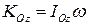Учитывая постоянство момента инерции для твёрдого тела, согласно теореме об изменении кинетического момента имеем

.

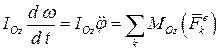Это и есть дифференциальное уравнение вращательного движения твёрдого тела вокруг неподвижной оси.

Частные случаи:

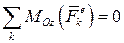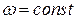· если , то , т.е. вращение равномерное;

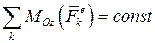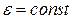· если , то , т.е. вращение равнопеременное.

Следует отметить, что дифференциальное уравнение вращательного движения аналогично по структуре дифференциальному уравнению поступательного движения твёрдого тела, откуда следует, что момент инерции во вращательном движении играет ту же роль, что и масса в поступательном движении, т.е. он характеризует инерционные свойства тела во вращательном движении. В этом смысле момент внешних сил аналогичен силам в поступательном движении.