Плоское движение

Из кинематики известно, что плоское движение твёрдого тела можно разложить на два простейших: поступательное вместе с полюсом и вращательное вокруг полюса. Примем за полюс центр масс тела. Тогда кинематические уравнения плоского движения запишутся в виде:

Для изучения плоского движения твёрдого тела достаточно составить три дифференциальных уравнения, связывающие величины 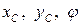с действующими на тело внешними силами.

Поступательная часть движения определяется дифференциальным уравнением поступательного движения (теоремой о движении центра масс)

Третье уравнение плоского движения получим, применив теорему об изменении кинетического момента относительно подвижной оси, проходящей через центр масс

.

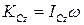Так как кинетический момент твёрдого тела относительно оси можно определить по формуле то, подставляя его в теорему, получим

.

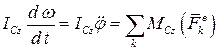Таким образом, дифференциальные уравнения плоского движения твёрдого тела имеют вид

.