Скорость точки в естественных координатах

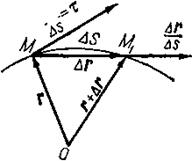
Движение точки будет задано в естественной форме, если известна ее траектория и закон (или уравнение) движения по траектории s=s (t), где s — дуговая координата точки (рис. 41), заданная как функция времени. Точка О — начало дуговых координат. Дуговая координата может быть положительной и отрицательной. Применяя формулу (11.13), получим

υ = r= lim

или υ = lim

то 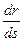является единичным вектором (или ортом) ка­сательной, который обозначим через τ. Действительно, 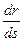- век­тор, направленный по секущей (рис. '41). В пределе получим вектор 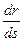, направленный по касательной

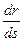=τ,

где τ по модулю равен единице. Таким образом, найдем

υ = τs.

Умножая скалярно обе части этого равенства на τ, получим

υ ∙ τ=τ ∙τs,

Или

υ = s,

где υ = υ cos (υ, τ) — проекция вектора скорости υ на касатель­ную τ, проведенную в рассматриваемой точке М в сторону возрас­тания дуговой координаты s.