Ускорение движения точки

Физическая величина, характеризующая быстроту изменения во времени скорости движения точки, называется ускорением. Рассмотрим два сколь угодно близких положения точки М и М 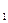на траектории. Скорость в точке М обозначим υ, а в точке М₁ — υ + Δυ (рис. 42). Геометрическое приращение вектора скорости Δυ за промежуток времени Δt найдем, построив в точ­ке М вектор, равный υ+ Δυ и соединив концы векторов υ и υ + Δυ. Отношение Δυ к Δt представит собой среднее ускорение ω_CP т.е.

w_Ср=

Вектор w_Ср имеет направление Δυ (рис, 42).

Переходя в (11.27) к пределу при Δt 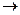0 , найдем ускорение w в данный момент времени

w=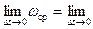
Если этот предел существует, то получим

w= =υ

Или

w=

так как υ=r. Таким образом,

w=υ=r

Из (11.28) видно, что ускорение точки равно нулю лишь тогда, когда скорость точки υ посто­янна как по величине, так и по направлению: это соответствует только прямолинейному и равно­мерному движению. В СИ за единицу ускорения принимают 1 м/с².

Так как ускорение в данной точке равно первой производной по времени от скорости, то оно направлено по касательной к годографу скорости. Проводя в каждой точке траектории векторы, соответ­ственно равные w₁, w₂, ..., w , определим направление ускорения в каждой точке (рис. 43). Конечно, приведенный способ определения направления ускорения точки представляет только теоретический интерес. На практике ускорение определяют более удобными мето­дами, о которых будет идти речь в следующих параграфах.