Скорость движения точки

Важной характеристикой движения точки является ее скорость. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.

Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.

Для равномерно-прямолинейного движения

Δ r = υΔ t,

где v– постоянный вектор.

Вектор vназывается скоростью прямолинейного и равномерного движения полностью его определяет.

Из соотношения (11.10) видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени. Из (11.10) имеем

υ=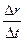

Направление вектора v указано на рис. 37.

Перейдем к рассмотрению неравномерного криволинейного дви­жения точки.

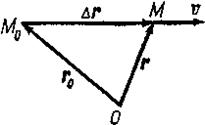
Пусть точка М произвольно движется по некоторой кривой. Пусть в момент t точка занимает положение М, а через весьма малый промежуток времени Δt она занимает положение М₁. Положение точки М определяется радиусом-вектором г, а положение точки М₁ — ради­усом-вектором г+Δг, равномерное прямолинейное движение точки из М в М^ можно охарактеризовать скоростью, равной отношению Δг к Δt, называемой средней скоростью:

υ_CP= .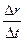

Вектор υ_CP совпадает с направлением вектора Δг.