Координатный способ. Этот способ определения движения точки состоит в том, что задаются координаты точки как функции времени, т. е.

х=х(t), у = у(t), z = z(t)

Между векторным и координатным способами задания движения точки существует следующая связь:

r=ix+jy+kz

где i,j,k — орты (или единичные векторы), соответственно направ­ленные по осям координат Ох, Оу, Оz.

На том же основании, что и г (t), функции х(t), у(t), z(t) являются однозначными, непрерывными, допускающими непрерывные производные.

Уравнения (П.2) являются уравнением траектории в параметрической форме. Исключая из уравнений (П.2) параметр t, получаем уравнение траектории в явной форме.

Если движение точки задано в полярных координатах

г=г(t), φ = φ(t),

где г — полярный радиус, φ — угол между полярной осью и по­лярным радиусом, то уравнения (П.4) выражают уравнение траекто­рии точки. Исключив параметр t, получим

г = г(φ).

3. Естественный способ. Если траектория точки известна зара­нее, то для определения закона движения точки в пространстве до­статочно задать положение точки на ее траектории. С этой целью одну из точек О на траектории принимают за начало отсчета дуговых координат, так как положение движущейся точки М определяется ее ориентированным расстоянием, которое отсчитывается по дуге траектории от выбранной точки отсчета (рис. 36). Следовательно, является функцией времени:

s = s(t).

Уравнение (11.6) определяет закон движения точки по траек­тории или закон изменения расстояния. Функция s= s (t) должна быть однозначной, непрерывной и дифференцируемой.

За положительное направление отсчета дуговой координаты s принимают направление движения точки в момент, когда она занимает положение О. следует помнить, что уравнение (11.6) не определяет закон движения точки в пространстве, так как для определения положения точки в пространстве нужно знать еще траекторию точки с начальным положением точки на ней и фиксированное положительное направление. Таким образом, движение точки считается заданным естественным способом, если известна траектория и уравнение (или закон) движения точки по траектории.

Важно заметить, что дуговая координата точки s отлична от пройденного точкой по траектории пути σ. При своем движении точка проходит некоторый путь σ, которой является функцией времени t. Однако пройденный путь σ совпадает с расстоянием s лишь тогда, когда функция

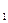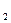s = s(t) монотонно изменяется со временем, т.е. при движении точки в одном направлении. Допустим, что точка М переходит из М в М . Положению точки в М 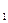соответствует время t 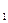, а положению точки в М 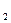- время t 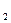. Разложим промежуток времени 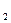t - t 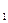на весьма малые промежутки времени Δ t 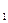(i = 1,2, …n) так, чтобы в каждый из них точка совершала движение в одном направлении. Соответствующее приращение дуговой координаты обозначим Δ s 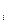. Пройденной точкой путь σ будет положительной величиной: σ =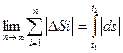

Если движение точки задано координатным способом, то пройденный путь определяется по формуле

σ=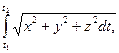

так как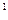

dσ=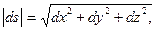

где dx=xdt, dy= ydt, dz=zdt.

Следовательно,

dσ = | ds| = .