Релятивистское преобразование скоростей

Пусть в неподвижной системе отсчета K положение материальной точки задано координатами x, y, z, t, а в подвижной K¢ – x¢, y¢, z¢, t¢. Система K¢ движется относительно K со скоростью V₀. Оси координат x и x¢ сонаправлены. Для проекций скоростей в этих системах отсчета получим

.

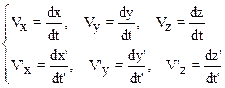Используя преобразования Лоренца (10.17) найдем дифференциалы координат и времени:

.

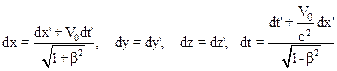Разделим первые три равенства (10.29) на четвертое:

.

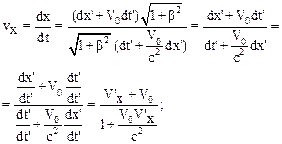
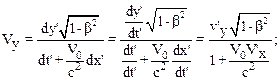
Аналогичным образом для обратного преобразования скоростей можно получить

.

Если тело движется вдоль оси x в системе K, то оно (см. рис. 10.1) движется также параллельно оси x¢ в системе K¢. Скорость тела в системе К равна V=V_x, в системе К¢ V¢=V¢_x. Тогда из (10.30) следует законсложения скоростей:

.

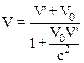При V¢<<c знаменатель выражения (10.34) стремится к 1. В этом пределе из (10.34) получаем, что V=V¢+V₀, что соответствует закону сложения скоростей по Галилею.

При V¢=c из выражения (10.34) получим:

,

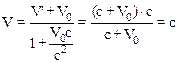то есть скорость света одна и та же в обеих инерциальных системах отсчета.