Релятивистский импульс
Классическое выражение для импульса частицы массой m
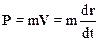 .
.
не инвариантно относительно преобразований Лоренца. Учитывая, что при малых скоростях собственное время частицы dt (время по часам, движущегося вместе с частицей) близко ко времени dt, измеренному по часам в неподвижной системе отчета, т. е. 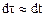 .
.
Запишем выражение для импульса (10.37) следующим образом:
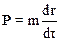 ,
,
где dr – вектор перемещения частицы.
Проверим инвариантность определения (10.37) по отношению к преобразованиям Лоренца. Рассмотрим процесс абсолютно упругого столкновения частиц с массами m1 и m2 в системах К и К¢, предполагая, что закон сохранения импульса справедлив в системе отсчета К. Запишем уравнение закона сохранения импульса:
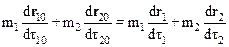 ,
,
здесь правая часть равенства представляет собой полный импульс системы частиц до столкновения, левая – после столкновения.
Проецируя соотношение (10.38) на оси x, y, z. Получаем:
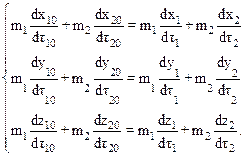
Перейдем к системе К¢, имея в виду что собственное время dt – инвариантно:
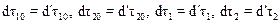
Проекции перемещений dr10 и dr20 в направлении оси x испытают лоренцево сокращение, в направлении осей y и z не изменятся:
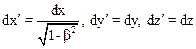 .
.
Разделим первое равенство системы (10.39) на 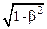 . Учитывая соотношения (10.40) и (10.41), получим:
. Учитывая соотношения (10.40) и (10.41), получим:
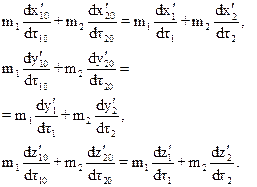
Возвращаясь к векторной записи, имеем:
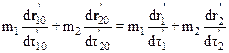 .
.
Таким образом, выражение для импульса (10.37) оказывается инвариантным относительно преобразований Лоренца, и, соответственно, закон сохранения импульса в СТО выполняется.
Так как собственное время частицы связано с временем t в системе К, относительно которой наблюдается движение тела, то для импульса в системе К получим:
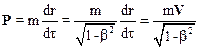 .
.
Очевидно, что при V<<c соотношение (10.43) переходит в выражение для классического импульсаP=mV. Иногда формулу (10.43) трактуют иначе: импульс, как в классической механике Ньютона, определяются выражением P=mV, но массутела считают не инвариантной величиной, а зависящей от скорости:
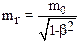 .
.
Масса mr, определяемая соотношением (10.44) называется релятивистской массой; инвариантной массой является m0 – масса покоя. Таким образом, релятивистский импульс принято записывать так:
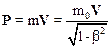 .
.
Дата добавления: 2015-08-08; просмотров: 1663;
