Генераторы импульсов

Схема одновибратора приведена на рис. 4.8, а. Он выполнен на двух элементах логики типа 2И-НЕ путем введения положительной обратной связи (выход второго элемента соединен с входом первого).

В исходном состоянии на выходе элемента Э2 имеется уровень “1”, а на выходе элемента Э1- “0”, так как на обоих его входах имеется “1”(запускающие импульсы представляют отрицательный перепад напряжения). При поступлении на вход запускающего отрицательного перепада напряжения на выходе первого элемента появится уровень “1”, т.е. положительный скачок, который через конденсатор С поступит на вход второго элемента. Элемент Э2 инвертирует этот сигнал и уровень “0” по цепи обратной связи подается на второй вход элемента Э1. На выходе элемента Э2 поддерживается уровень “0” до тех пор, пока не зарядится конденсатор С до уровня U_{c пор} = U¹ - U_пор, а напряжение на резисторе R не достигнет порогового уровня U_пор (рис. 4.8, б).

Длительность выходного импульса одновибратора может быть определена с помощью выражения

,

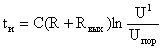где R_вых - выходное сопротивление первого элемента. U_пор - пороговое напряжение логического элемента.

Несимметричный мультивибратор. На базе логических элементов можно построить различные генераторы импульсов. Наиболее широкое применение в цифровых устройствах нашли два типа - несимметричный и симметричный мультивибраторы. В несимметричном мультивибраторе (рис. 4.9, а) резистор R выводит в усилительный режим первый инвертор, а выходное напряжение этого инвертора должно удерживать в режиме усиления второй инвертор. Положительная обратная связь через конденсатор С вызовет мягкое (не нуждающееся в первоначальном толчке) самовозбуждение автоколебательного релаксационного процесса. Период Т импульсов, вырабатываемых мультивибратором, определяется в первом приближении постоянной времени t = RC (Т = а t, где а обычно имеет значение 1...2). Частоту следования импульсов можно оценить (с точностью до 10 %) из выражения f = 1/2RC.

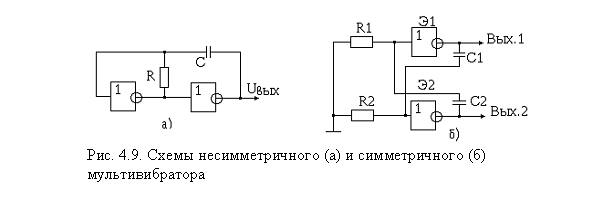
Симметричный мультивибратор. Схема симметричного мультивибратора показана на рис. 4.9, б. Симметричность выходных импульсов может быть достигнута при выполнении условий: R1 = R2; C1 = C2. Период следования импульсов Т определяется как сумма двух времен заряда конденсаторов, т.е.

Т = t_зар1 + t_зар2 ,

где t_зар1 = t₁ ln(U¹/U_пор); t_зар2 = t₂ ln(U¹/U_пор).

Значения t₁ и t₂ определяются с учетом выходных сопротивлений инверторов R_{вых Э1} , R_{вых Э2}

t₁ = С₁ (R₂ + R_{вых Э1})

t₂ = С₂ (R₁ + R_{вых Э2}).

Частота следования выходных импульсов симметричного мультивибратора определяется из соотношения:

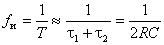
Генераторы линейно изменяющего напряжения (ГЛИН). ГЛИН представляют собой электронные устройства, выходное напряжение которых в течение некоторого времени изменяется по линейному закону. Часто такое напряжение меняется периодически. В этом случае ГЛИН называется генератором пилообразного напряжения (ГПН) или генератором напряжения треугольной формы (рис. 4.10, а, б). Если напряжение меняется от минимального значения к максимальному (по абсолютной величине), то его называют линейно-нарастающим напряжением. Если меняется от максимального значения к минимальному - линейно-падающим.

ГЛИН нашли широкое применение в отклоняющих системах осциллографов, телевизоров, в радиолокации, в преобразователях “напряжение-временной интервал”, широтно-импульсных модуляторах и т.д.

ГЛИН строятся на принципе заряда и разряда конденсатора. Схема простейшего ГПН, работающего по принципу заряда конденсатора, показана на рис. 4.10, в. Она состоит из времязадающего конденсатора С, резистора R_к и транзисторного ключа VT1. На вход транзисторного ключа подается последовательность прямоугольных импульсов с заданным интервалом между импульсами и длительностью (рис. 4.10, г). Когда на базе транзистора нулевое напряжение (промежуток времени между импульсами), транзистор закрыт и происходит заряд конденсатора через резистор R_к. Если постоянная времени цепи R_к C достаточно большая, т.е. существенно больше периода следования прямоугольных импульсов, напряжение на конденсаторе нарастает линейно. Заряд конденсатора продолжается до поступления импульса, открывающего транзистор VT. Когда транзистор открывается, начинается процесс разряда конденсатора. Интервал времени между отпирающими импульсами должен быть достаточным для полного разряда конденсатора С.

Напряжение на конденсаторе изменяется по закону:

,

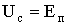
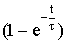где t = RC - постоянная времени цепи, состоящей из R_к и С; t - текущее значение времени, когда t=0, U_с = Е_п(1- 1) = 0.

Известно, что функцию е^х можно представить в виде степенного ряда

.

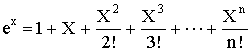Для значений Х<<1 функцию можно определить первыми двумя членами ряда

е^х = 1+Х,

тогда, используя это выражение для случая заряда конденсатора при t<<t, определяем напряжение на конденсаторе

U_c = E_п(1- ,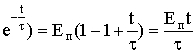

где t/t <<1.

Очевидно, что в случае использования этого процесса в ГПН, t = t_и = t_зар; t = R_к С, тогда

.

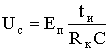Линейно изменяющееся напряжение U_c (t) характеризуется рядом параметров:

- длительностью прямого хода t_пр, т.е. временем, в течение которого конденсатор заряжается через сопротивление R_к до напряжения U_c;

- длительностью обратного хода t_o (время восстановления) - это время, в течение которого происходит разряд конденсатора;

- периодом повторения линейно изменяющегося напряжения (пи-лообразных импульсов) T = t_o + t_пр;

- амплитудой пилообразных импульсов U_m;

- коэффициентом нелинейности g.

Одним из самых важных параметров ГЛИН являетсякоэффициент нелинейности. Для определения g воспользуемся известным утверждением, что линейная функция характеризуется постоянством производной во всех её точках, поэтому отклонение от линейного закона можно оценить коэффициентом нелинейности. Нелинейность определяется максимальным отклонением реальной формы сигнала от идеальной линейной формы. Коэффициент нелинейности находят как отношение изменений производных функции в начале и в конце процесса нарастания

.

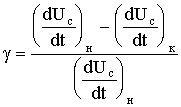Учитывая, что dU_c/dt = i_c/C, где i_c - ток заряда конденсатора, можно получить удобное для расчетов выражение

,

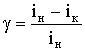где i_н - ток заряда конденсатора в начале процесса (импульса); i_к - ток заряда к моменту окончания импульса.

Если пренебречь обратным током транзистора и током утечки конденсатора i_н можно определить как

i_н = Е_п / R_к.

В конце импульса напряжение, заряжающее конденсатор С, будет меньше напряжения источника питания на величину U_m, следовательно, ток в конце будет определяться как

i_к = (Е_п - U_m) / R_к.

Так как при t_пр <<t U_m = U_c = E_п t_пр/ RC, окончательное выражение коэффициента нелинейности будет иметь вид

.

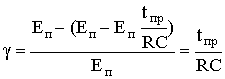Простейший генератор линейного напряжения характеризуется также коэффициентом использования напряжения источника питания

x = U_m / E_п.

Если подставить значение U_m в выражение для коэффициента использования напряжения источника питания, получим

x = .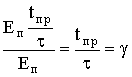

Из полученного выражения для коэффициента нелинейности следует, что чем лучше линейность пилообразного напряжения, тем меньше амплитуда напряжения ГЛИН. Например, если напряжение источника питания 10 В, для получения коэффициента нелинейности g = 1 % амплитуда напряжения импульсов ГПН не должна превышать 0,1 В.

Для повышения коэффициента использования напряжения питания при малых значениях коэффициента нелинейности применяются стабилизаторы постоянного тока (ГСТ). Действительно, из выражения для g видно, что при обеспечении постоянства тока заряда (для линейно падающего напряжения - тока разряда) i_н = i_к, следовательно ®g0.

Схема простого генератора пилообразного напряжения со стабилизатором тока в цепи разряда конденсатора показана на рис. 4.11, а. Заряд конденсатора осуществляется через транзистор VT1 и сопротивление R_к. За время заряда напряжение на конденсаторе достигает практически напряжения источника питания. Когда приходит на базу транзисторов нулевой уровень, первый транзистор закрывается, а транзистор VT2 переходит в режим генератора стабильного тока (ГСТ) и через него протекает стабильный постоянный ток разряда конденсатора (рис. 4.11, б).

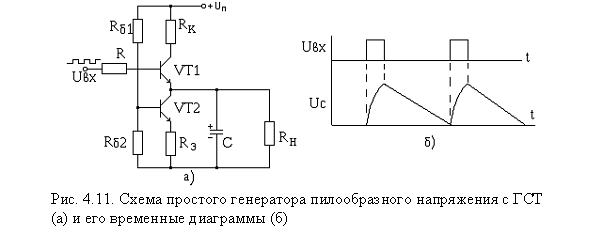
При определении коэффициента нелинейности импульсов этого генератора пилообразного напряжения необходимо учитывать влияние сопротивления нагрузки R_н на процесс разряда конденсатора. Ток через сопротивление нагрузки обусловлен напряжением на конденсаторе и в конце разряда он равен нулю, так как к концу разряда U_c = 0. С учетом высказанных соображений можно получить выражение для коэффициента нелинейности ГПН с генератором стабильного тока.

.

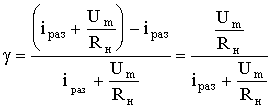Из полученного выражения следует, что для уменьшения g желательно использовать высокоомные нагрузки или же уменьшать амплитуду импульса сигнала.

5.1. Цифро-аналоговые преобразователи (ЦАП)

ЦАП служит для преобразования цифровой информации в аналоговую форму, т.е. выходной сигнал ЦАП в общепринятых единицах измерения тока или напряжения (мВ, В, мА) соответствует численному значению входной кодовой комбинации.

Например, при подаче на вход ЦАП кодовой комбинации (в десятичном эквиваленте) равной 150 на его выходе при этом имеется напряжение 1500 мВ, это значит, что изменение значения входной кодовой комбинации (входного числа) на единицу приводит к изменению выходного напряжения на 10 мВ. В этом случае мы имеем ЦАП с шагом преобразования цифровой информации 10 мВ. Величина напряжения, соответствующая одной единице цифровой информации, называется шагом квантования Du_кв. При подаче на вход ЦАП последовательной цифровой комбинации, меняющейся от 0 до N, на его выходе появится ступенчато-нарастающее напряжение (рис. 5.1). Высота каждой ступени соответствует одному шагу квантования Du_кв.

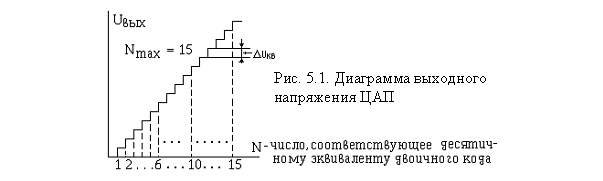
Если число входной кодовой комбинации соответствует N, то выходное напряжение U_{вых ЦАП} = ND´u_кв. Таким образом можно вычислить значение выходного напряжения для любой входной кодовой комбинации. Нетрудно убедиться в том, что Du_кв является масштабным коэффициентом преобразователя, имеющим размерность тока или напряжения (так как цифровая комбинация на входе ЦАП размерности не имеет). Обычно, значение Du_кв выбирают кратным десяти, что облегчает процесс пересчета соответствия преобразованного и исходного сигналов. Так как Du_кв определяет минимальное значение выходного напряжения аналогового сигнала U_{вых мин.} = Du_кв, при выборе его значения необходимо учитывать также шумовые факторы, погрешности усиления масштабирующих усилителей и компаратора.

Основные параметры ЦАП. Точность преобразования и качество работы ЦАП характеризуют следующие параметры: относительная разрешающая способность, абсолютная разрешающая способность, абсолютная погрешность преобразования, нелинейность преобразования, дифференциальная нелинейность, скорость преобразования (время одного преобразования) и максимальная частота преобразования.