Относительностьдлины

Пусть (см. рис. 10.4) в подвижной системе отсчета К¢ длина некоторого стержня, расположенного вдоль оси х, равна L₀ (L₀= x¢₂-x¢₁). ¢. Определим длину L=x₂-x₁стержня в системе К, относительно которой он движется со скоростью V₀ вдоль оси х вместе с системой К¢.

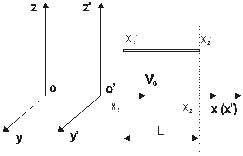
Рис. 10.4. Неподвижная (x,y,z,o) и подвижная (x¢,y¢,z¢,o¢) системы отсчета

Так как стержень движется относительно К со скоростьюV₀, то используя преобразование Лоренца, запишем

,

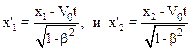следовательно, длина стержня в подвижной системе отсчета равна:

.

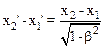Соотношение (10.29) указывает на то, что длины L₀ и L не равны между собой. Из соотношения (10.20) следует:

.

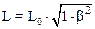Таким образом, длина стержня в системе, относительнокоторой он движется, меньше его длины в системе относительно которой он покоится. Явление уменьшения размеров тел в направлении движения называется лоренцевым сокращением длины. Очевидно, лоренцево сокращение длины тем больше, чем больше скорость V движения системы отсчета, как это показано на рисунке 10.3.

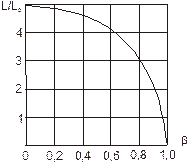
Рис. 10.5. Лоренцево сокращение длины как функция релятивистского множителя b=V/c

Укажем, что заметить или зафиксировать лоренцево сокращение длины нельзя даже при скорости V близкой к скорости света. Изображение предмета на сетчатке глаза – результат одновременного воздействия на сетчатку света, пришедшего от различных точек предмета. Очевидно, что для такого одновременного воздействия импульсы, пришедшие от точек, находящихся на различных расстояниях от наблюдателя, должны быть испущены не одновременно. Оптическое изображение оказывается искаженным, но это искажение, компенсирует лоренцево сокращение длин.