Интервал

Пусть событие Р происходит в некоторой точке (x,y,z) инерциальной системы отсчета в момент времени t_К. Это событие в четырехмерном пространстве-времени (x,y,z,сt) можно представить точкой, называемой мировой точкой. С течением времени координаты материальной точки изменяются, и ее мировая точка описывает в четырехмерном пространстве-времени траекторию, называемую мировойлинией.

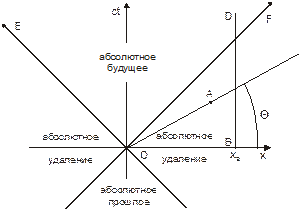
В частном случае двух координат (см. рис. 10.1), мироваяточка – это точка на плоскости (х, ct); траектория точки – мировая линия – линия на этой плоскости. Так, траектория материальной точки В, неподвижной (x=const) в ИСО К, представляет собой прямую BD, параллельную оси времени сt.

Рис. 10.1. События абсолютно прошедшие и абсолютно будущие по отношению к событию О

Пусть мировая точка А изображает некоторое событие. Проведем через начало координат системы К прямую ОА, угловой коэффициент которой равен tgq=ct/x, где х=Vt. Прямая, уравнение которой имеет вид ct=хtgq представляет собой мировую линию материальной точки движущейся с постоянной скоростью V. Угловой коэффициент линии ОА равен tgq=c/V. Отсюда следует, что:

.

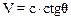При q>p/4 с материальной точкой А можно связать подвижную систему отсчета К¢, а ось ОА принять за ось х¢. Положение второй оси координат найдем из условия, что во всех ее точках х¢ равно нулю, что выполняется (см. (10.24)) при х=tV/c. Таким образом, подвижная система координат (см. рис. 10.2) имеет осями мировые линии х¢ и ct¢.

Рис. 10.2. Диаграмма Минковского

Отметим, что изображенные на рисунке 10.1 биссектрисы координатных углов – OF и OE, тангенсы угла наклона которых равны 1 и –1 представляют собой мировые линии световых импульсов распространяющихся вдоль оси х и против нее.

Очевидно, что события О и А (см. рис. 10.2) в системе К не являются одновременными. В системе К¢ они происходят одновременно (в момент t¢=0). Рисунок 10.1 показывает, как СТО позволяет строго упорядочить события во времени. Рассмотрим световой сигнал, испущенный в точке x₁ в момент времени t₁ (событие 1) и принятый в точке x₂ в момент времени t₂ (событие 2). Если время распространения света равно t₁₂, то расстояние между источником и приемником света равно

.

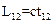Соответствующий этому событию интервал есть

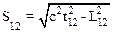
Ниже (параграф 10.1.2) будет доказано, что интервал величина инвариантная относительно преобразований координат Лоренца.

Если расстояние L₁₂ между событиями больше ct₁₂, то подкоренное выражение меньше нуля и интервал S₁₂ – мнимый. Мнимые интервалыназываются пространственно-подобными. Пространственно-подобные интервалы разделяют события, которые ни в одной системе отсчета не могут происходить в одной точке. Действительно, в этом случае L₁₂ = 0, и, как следует из определения (10.3) интервал становится действительным. События 1 и 2 разделенные пространственно-подобным интервалом не могут быть причинно связаны, так как сигнала, распространяющегося со скоростью, большей скорости света, не существует. С другой стороны всегда можно выбрать такую систему отсчета, в которой t₁₂=0, т. е. события разделены пространственно-подобным интервалом и происходят в одно и то же время – одновременно.

Вещественный интервалS₁₂ называется времениподобным. Для того, чтобы интервал был вещественным необходимо выполнение условия L₁₂<ct₁₂. в этом случае события 1 и 2 могут совпадать в пространстве, но не могут происходить одновременно. Для рассматриваемых событий величины t₁₂ и t¢₁₂ имеют один и тот же знак. Это означает, что если событие 2 происходит позже события 1 в некоторой системе отсчета, то оно наступит позже в любой другой системе. Последовательность событий не меняется в любой системе отсчета, а это значит, что они могут находиться в причинно-следственной связи. СТО установила, что причинно-следственная связь является следствием конечной скорости распространения сигнала.