Доверительный интервал. Доверительная вероятность.

2. Расчёт и построение доверительных интервалов.

3. Пример сравнения средних арифметических, расчёта и построения доверительного интервала.

1.

Чтобы статистически оценить искомое истинное значение характеристики Q, поступают следующим образом:

1) Задаются некоторой достаточно большой вероятностью p (например, p = 0,9; 0,95; 0,99; 0,999), чтобы событие, заключающееся в нахождении искомого значения Q с этой вероятностью в соответствующем интервале можно было считать статистически достоверным. Эту вероятность называют доверительной вероятностью. В спортивных исследованиях обычно принимают p = 0,95 (иногда 0,99).

2) Затем для заданной величины p рассчитывают по формулам математической статистики нижнюю Q₁ и верхнюю Q₂ границы интервала J_p.

Доверительным интервалом J_p называют случайный интервал (Q₁, Q₂), который накрывает неизвестную характеристику Q с доверительной вероятность p.

Границы доверительного интервала J_p называют:

Q₁ = Q* - e₁¾нижней доверительной границей;

Q₂ = Q* - e₂¾верхней доверительной границей.

Значения e₁ и e₂ могут совпадать (при симметричном распределении Q*) и быть разными (при несимметричном распределении Q*). Они характеризуют точность, а вероятность p¾надежность определения Q. Между надежностью и точностью существует обратная зависимость: чем выше надежность, тем ниже точность определения Q и наоборот.

С увеличением числа измерений при заданном p повышается точность определения Q (уменьшаются e₁ и e₂).

Для точного расчета границ доверительного интервала необходимо знать закон распределения выборочной характеристики Q*.

2. Задача определения доверительных интервалов для оценки генерального среднего арифметического значения x_г нормального распределения решена математической статистикой для следующих двух случаев:

а) генеральная дисперсия известна;

б) генеральная дисперсия неизвестна.

Рассмотрим второй случай.

В этом случае искомое генеральное среднее арифметическое находится в следующем доверительном интервале:

,

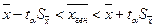где 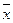– среднее арифметическое значение выборки; t_a – величина, которая находится по таблицам распределения Стьюдента в зависимости от числа степеней свободы k = n - 1, уровня значимости a; 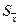– стандартная ошибка среднего арифметического, рассчитывается по формуле:

.

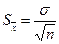Примечание: В практике научных исследований, когда закон распределения малой выборочной совокупности (n < 30) неизвестен или отличен от нормального, пользуются вышеприведенной формулой для приближенной оценки доверительных интервалов.

3. Для рассмотрения этого вопроса используется пример с двумя группами велосипедистов, прошедших подготовку с использованием разных методик (Гинзбург Г.И., Киселев В.Г. Расчетно-графические работы по спортивной метрологии. – Минск: БГОИФК, 1984. – С. 38 – 43)

Контрольные вопросы для самопроверки:

1. Что такое доверительный интервал, доверительная вероятность?

2. Порядок построения доверительного интервала.

3. В каких случаях можно точно определить границы доверительного интервала?

Литература:

1. Основы математической статистики. Уч. пособие для ин-тов физической культуры (под общ. ред. В.С. Иванова). – М.: Физкультура и спорт, 1990. – С. 74 – 78.

2. Рукавицына С.Л., Волков Ю.О., Солтанович Л.Л. Спортивная метрология. Проверка эффективности методики тренировки с применением методов математической статистики. Практикум для студентов БГУФК. – Минск: БГУФК, 2006. – С. 67 – 68.

3. Гинзбург Г.И., Киселев В.Г. Расчетно-графические работы по спортивной метрологии. – Минск: БГОИФК, 1984. – С. 35 – 51.