Сравнение средних попарно-зависимых выборок.

1. В математической статистике разработан ряд критериев (параметрических и непараметрических) для сравнения средних арифметических.

Выбор критерия зависит от следующих условий:

1) объёма выборки (большие или малые);

2) законов распределения исследуемых совокупностей (нормальные, другие);

3) степени независимости выборок (зависимые, независимые);

4) известны или неизвестны генеральные дисперсии;

5) одинаковы или различны генеральные дисперсии;

6) возможна ли количественная или только качественная оценка рассматриваемого явления.

К параметрическим критериям для сравнения двух средних арифметических относятся критерии t для независимых и попарно зависимых выборок, имеющие распределение Стьюдента, а также критерий z, имеющий нормальное распределение. Последний разработан для сравнения двух средних арифметических независимых нормальных генеральных совокупностей, дисперсии которых известны. Так как в задачах из области физической культуры и спорта дисперсии генеральных совокупностей обычно неизвестны, критерий z для малых выборок не используется. Его рекомендуется использовать в качестве приближённого критерия для сравнения больших независимых выборок, имеющих любой закон распределения, так как для больших выборок (n≥30) выборочные средние арифметические распределены приближённо нормально, а выборочные дисперсии приближённо равны генеральным дисперсиям.

Из существующих непараметрических критериев наиболее мощными являются X-критерий Ван дер Вардена для независимых выборок и U-критерий Уилкоксона для попарно зависимых выборок.

2. При сравнении средних независимых выборок рекомендуется поступать следующим образом:

1) Каждая в отдельности выборка проверяется на нормальность распределения по критерию Шапиро и Уилка

.

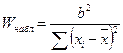В случае, если обе выборки распределены нормально, следует переходить к следующему пункту, в противном случае – к п. 4.

2) Сравниваются дисперсии выборок

.

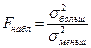В случае равенства дисперсий следует переходить к следующему пункту, в противном случае – к п. 4.

3) Для сравнения средних арифметических используется критерий Стьюдента

.

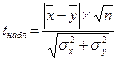Сравнение окончено.

4) Для сравнения средних арифметических используется критерий Ван дер Вардена

.

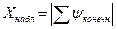Сравнение окончено.

3. При сравнении средних попарно зависимых выборок рекомендуется поступать следующим образом:

1) Составляется выборка разностей парных значений .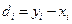

2) Составленная выборка проверяется на нормальность распределения по критерию Шапиро и Уилка. В случае, если выборка распределена нормально, переходим к следующему пункту, в противном случае – к п. 4.

3) Для сравнения средних арифметических используется критерий Стьюдента

.

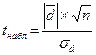Сравнение окончено.

4) Для сравнения средних арифметических используется U-критерий Уилкоксона. Сравнение окончено.

Контрольные вопросы для самопроверки:

1. Какие условия определяют выбор критерия для сравнения средних арифметических двух выборок?

2. Какие параметрические и непараметрические критерии используются для сравнения средних арифметических двух выборок?

3. Какие критерии в каких случаях используются для сравнения средних независимых выборок?

4. Какие критерии в каких случаях используются для сравнения средних попарно зависимых выборок?

Литература:

1. Основы математической статистики. Уч. пособие для ин-тов физической культуры (под общ. ред. В.С. Иванова). – М.: Физкультура и спорт, 1990. – С. 90 – 103.

2. Рукавицына С.Л., Волков Ю.О., Солтанович Л.Л. Спортивная метрология. Проверка эффективности методики тренировки с применением методов математической статистики. Практикум для студентов БГУФК. – Минск: БГУФК, 2006. – С. 62.

3. Гинзбург Г.И., Киселев В.Г. Расчетно-графические работы по спортивной метрологии. – Минск: БГОИФК, 1984. – С. 34 – 35.