Распределение Больцмана и вероятность.

Распределение Больцмана представляет собой отношение числа частиц, обладающих определенной потенциальной энергией, или, что то же самое, находящихся в некоторой точке силового поля, к полному числу частиц в газе. Тот факт, что та или иная частица оказывается в определенной точке пространства, есть событие случайное, потому что оно является следствием хаотического теплового движения. Поэтому можно утверждать, что распределение Больцмана представляет собой вероятность того, что некоторое число частиц будет иметь заданное значение потенциальной энергии. Рассмотрим основные свойства вероятности. Теория вероятности изучает явления, которые имеют случайный характер. Случайным называется событие, которое нельзя предсказать с определенностью. Этим оно отличается от достоверного события. Пример случайного события — приход определенной молекулы в заданную точку в результате беспорядочного теплового движения в газе частиц. Пример достоверного события — приход той же молекулы в заданную точку в результате движения по траектории с заданной скоростью без столкновений. В первом случае появления меченой молекулы в заданной точке можно ожидать с некоторой вероятностью.

Вероятностью P(A) некоторого события A называется частота появления данного события A в общем числе событий A. Ясно, что вероятность есть положительная величина. Из ее определения следует, что 0 <= P <= 1. Если событие достоверно, то P = 1. Если событие не может произойти вообще, то P = 0.

Вероятность сложного события, состоящего из двух независимых событий, равна произведению вероятностей каждого из независимых событий.

Случайное событие, в частности, может состоять в том, что какая-либо физическая величина имеет определенное, но произвольное значение. Такие величины называются случайными. Случайные величины могут принимать как дискретные, так и непрерывные значения.

Если случайная физическая величина принимает непрерывный ряд значений x, то вероятность dP того, что величина x находится в бесконечно малом промежутке между x и x + dx, равна 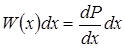. Функция W(x) называется плотностью вероятности.

Очевидно, .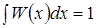

Предположим, что случайная величина принимает ряд значений x₁, x₂,..., x_N, с вероятностями P₁, P₂,..., Р_N. Тогда ее среднее значение определяется соотношением

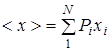. (2.12)

Если x меняется непрерывно и плотность вероятности есть W(x), то среднее значение

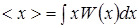. (2.13)

Аналогично можно определить средние значения и других величин: среднего квадратичного значения случайной величины

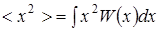; (2.14)

среднего значения произвольной функции случайной величины

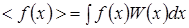(2.15)

и т. д.

Зная, что плотность вещества по определению 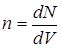, формулу

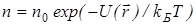можно записать в виде:

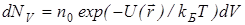. (2.16).

Здесь dN_V — число частиц, заключенных в элементе объема dV и имеющих заданное значение потенциальной энергии U(r). Полное число частиц в газе можно найти, суммируя по всему объему, занятому газом:

. (2.17)

Таким образом, в газе, находящемся во внешнем поле, характеризуемом потенциальной энергией U(r), устанавливается неравномерное распределение частиц в пространстве. Число частиц максимально в состоянии с минимальной потенциальной энергией и убывает вдали от этой точки. Эта неравномерность обусловлена случайным блужданием частиц в координатном пространстве, которое является следствием теплового движения в газе при конечной температуре.