Некоторые эмпирические закономерности рассеяния характеристик усталости
В ходе многих исследований было установлено, что рассеяние долговечности увеличивается с уменьшением уровня амплитуды напряжения при испытании и с увеличением средней долговечности образцов как из черных, так и из цветных сплавов. На рис. 4.1 и 4.2 показаны эти зависимости для конструкционных алюминиевых сплавов АД33, АВ, Д16 и В95 различных плавок. Каждая точка была построена по результатам испытаний на усталость при изгибе с вращением десятков и сотен гладких образцов [1].

Рис. 4.1. Зависимость среднего квадратического отклонения логарифма долговечности от уровня амплитуды цикла напряжений и среднего значения логарифма числа циклов до разрушения образцов: 1 — сплав АД33, 2 — сплав АВ
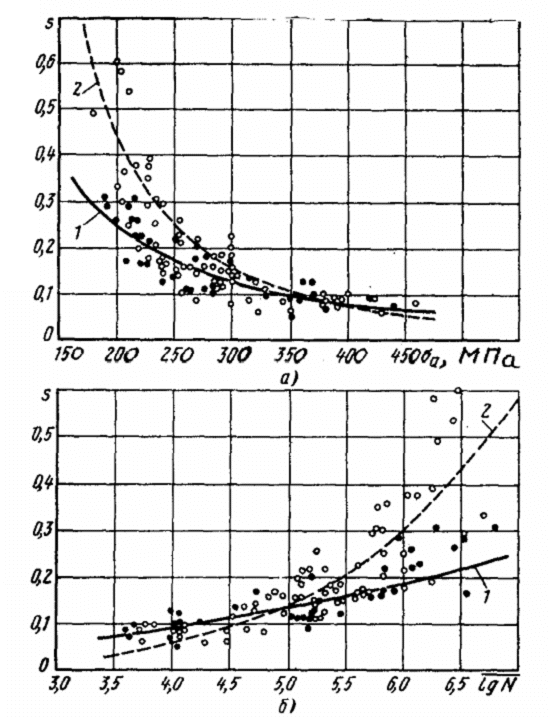
Рис. 4.2. Зависимость среднего квадратического отклонения логарифма долговечности от уровня амплитуды цикла напряжений и среднего значения логарифма числа циклов до разрушения образцов: 1-сплав Д16, 2- сплав В95.
Корреляционный анализ приведенных выше и многих других результатов испытаний на усталость позволяет считать в первом приближении, что между средним квадратическим отклонением логарифма числа циклов до разрушения 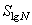 и уровнем амплитуды цикла напряжений
и уровнем амплитуды цикла напряжений 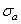 и средним значением логарифма долговечности
и средним значением логарифма долговечности 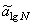 существует степенная зависимость в виде
существует степенная зависимость в виде
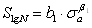 (4.3)
(4.3)
и
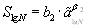 (4.4)
(4.4)
где 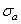 — амплитуда цикла напряжений при испытании, b1,
— амплитуда цикла напряжений при испытании, b1, 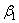 , b2, и
, b2, и 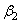 — параметры уравнений (4.3) и (4.4).
— параметры уравнений (4.3) и (4.4).
Подтверждением этого служит таблица 4.1, где наряду со значениями параметров уравнений (4.3) и (4.4) для деформируемых алюминиевых сплавов АД33, АВ, Д16 и В95 приведены значения эмпирического коэффициента корреляции r между величинами 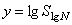 и
и 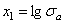 ,
, 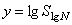 и
и 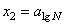 , а также средней квадратической ошибки коэффициента корреляции Sr [1]. Для всех рассмотренных случаев абсолютное значение коэффициента корреляции, как следует из таблицы 4.1, существенно выше своей среднеквадратической ошибки, что свидетельствует о достаточно тесной линейной зависимости между случайными величинами y и x1, y и x2, т.е. о существовании соотношений (4.3) и (4.4).
, а также средней квадратической ошибки коэффициента корреляции Sr [1]. Для всех рассмотренных случаев абсолютное значение коэффициента корреляции, как следует из таблицы 4.1, существенно выше своей среднеквадратической ошибки, что свидетельствует о достаточно тесной линейной зависимости между случайными величинами y и x1, y и x2, т.е. о существовании соотношений (4.3) и (4.4).
Для указанных выше алюминиевых сплавов графики уравнений (4.3) и (4.4) приведены на рис. 4.1 и 4.2.
Таблица 4.1. Значения параметров уравнений (4.3) и (4.4)
| сплав | число исследованных вариантов плавок и размеров профилей | число уровней амплитуд напряжений | число испытанных образцов | уравнение (4.3) | уравнение (4.4) | ||||||
| b1 | 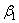
| r1 | 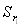
| b2 | 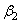
| r2 | 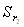
| ||||
| АД33 | 2,79 | -0,535 | -0,51 | 0,13 | 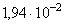
| 1,244 | 0,45 | 0,14 | |||
| АВ | 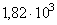
| -1,719 | -0,68 | 0,07 | 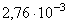
| 2,509 | 0,67 | 0,08 | |||
| Д16 | 
| -1,645 | -0,75 | 0,07 | 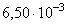
| 1,881 | 0,67 | 0,09 | |||
| В95 | 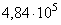
| -2,625 | -0,94 | 0,01 | 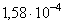
| 4,220 | 0,69 | 0,06 |
Существование зависимостей (4.3) и (4.4) наиболее надежно подтверждает корреляционный анализ результатов испытаний на усталость большой партии образцов (n = 1590) из сплава АВ одной плавки [1] (таблица 4.2).
Таблица 4.2. Корреляционный анализ результатов испытаний на усталость образцов из сплава АВ одной плавки
| уравнение (4.3) | уравнение (4.4) | ||||||

| 
| 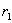
| 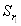
| 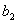
| 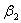
| 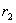
| 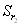
|
| -1,473 | -0,93 | 0,05 | 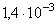
| 2,944 | 0,99 | 0,01 |
Абсолютное значение эмпирического коэффициента корреляции в этом случае достигает величины 0,93-0,99, а его средняя квадратическая ошибка не превышает 0,05, что говорит о тесной связи среднего квадратического отклонения логарифма долговечности с уровнем амплитуды цикла напряжений и средним значением величины 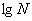 .
.
Характеристики рассеяния предела ограниченной выносливости этой серии образцов из сплава АВ приведены в таблице 4.3.
Таблица 4.3. Характеристики рассеяния пределов ограниченной выносливости образцов из сплава АВ
| Характеристика рассеяния | База испытаний в циклах | |||||
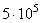
| 106 | 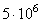
| 107 | 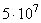
| 108 | |
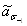 , МПа , МПа
| 195,1 | 176,5 | 144,9 | 135,5 | 118,4 | 113,8 |
 , МПа , МПа
| 18,2 | 15,9 | 12,5 | 10,7 | 9,4 | 8,9 |
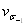
| 0,093 | 0,090 | 0,086 | 0,079 | 0,079 | 0,078 |
Среднее квадратическое отклонение предела выносливости для базы N=5×105 циклов составляет 18,2 МПа, а для базы N=108 циклов — 8,9 МПа (таблица 4.3), т. е. снижается почти в два раза, в то время как коэффициент вариации предела выносливости практически остается на одном уровне (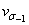 =8-9 %).
=8-9 %).
Следует отметить, что коэффициент вариации пределов ограниченной выносливости существенно выше, чем коэффициент вариации предела прочности, который у рассматриваемого сплава составляет 0,01-0,03.
Корреляционный анализ полученных результатов (таблица 4.3) дает основание считать, что между средним квадратическим отклонением предела выносливости и базой испытания существует зависимость в виде
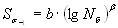 (4.5)
(4.5)
где 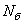 - база испытаний.
- база испытаний.
Значения параметров b и 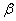 для исследованного сплава равны соответственно 73,3 и -2,14. Коэффициент корреляции между величинами
для исследованного сплава равны соответственно 73,3 и -2,14. Коэффициент корреляции между величинами 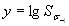 и
и 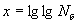 составляет 0,99 при средней квадратической ошибке 0,01, что подтверждает существование степенной зависимости типа (4.5).
составляет 0,99 при средней квадратической ошибке 0,01, что подтверждает существование степенной зависимости типа (4.5).
При решении практических задач, связанных с оценкой долговечности элементов конструкций, эффективности новых технологий и т. д., из всех ранее перечисленных характеристик рассеяния усталостных свойств наиболее широкое применение получило среднее квадратическое отклонение логарифма числа циклов до разрушения 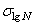 . Однако, как уже было показано, величина
. Однако, как уже было показано, величина 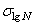 в значительной степени зависит от уровня амплитуды цикла напряжений при испытании на усталость и от средней долговечности
в значительной степени зависит от уровня амплитуды цикла напряжений при испытании на усталость и от средней долговечности 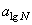 . Поэтому для надежного обоснования указанных зависимостей требуются испытания на усталость большого объема образцов.
. Поэтому для надежного обоснования указанных зависимостей требуются испытания на усталость большого объема образцов.
Существенно более стабильной характеристикой рассеяния усталостных свойств для различных участков кривой усталости, как показывает анализ результатов массовых испытаний на усталость, является коэффициент вариации предела ограниченной выносливости. Как видно из данных таблицы 4.3, а также из рис. 4.3, где представлены результаты испытаний образцов различных размеров и с разной степенью концентрации напряжений для широкого круга литейных и деформируемых сплавов на алюминиевой и магниевой основах, коэффициент вариации предела ограниченной выносливости практически не зависит от базы испытаний. Корреляционный анализ указанных результатов показал, что эмпирический (выборочный) коэффициент корреляции между коэффициентом вариации предела ограниченной выносливости и базой испытаний составляет лишь величину r = -0.10, которая соизмерима с его средней квадратической ошибкой Sr = 0.07.
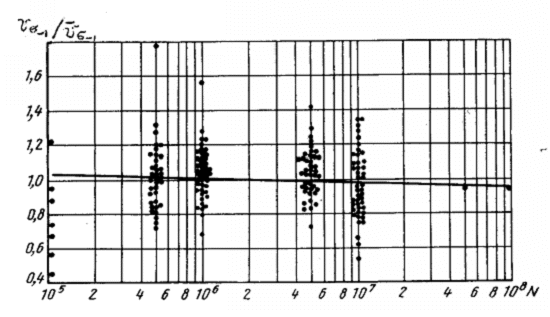
Рис. 4.3. Значения отношений выборочного коэффициента вариации предела ограниченной выносливости 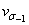 для заданной базы к среднему значению
для заданной базы к среднему значению 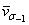 коэффициента вариации для каждого сплава, его состояния и геометрии усталостных образцов.
коэффициента вариации для каждого сплава, его состояния и геометрии усталостных образцов.
Независимость коэффициента вариации предела ограниченной выносливости от базы испытаний, как это вытекает из теории вероятностей, равнозначна постоянству среднего квадратического отклонения величины  для различных базовых долговечностей, что находится в достаточно удовлетворительном соответствии с результатами опытов. Анализ опытных данных показал, что выборочное среднее квадратическое отклонение величины
для различных базовых долговечностей, что находится в достаточно удовлетворительном соответствии с результатами опытов. Анализ опытных данных показал, что выборочное среднее квадратическое отклонение величины  для гладких и надрезанных образцов различных размеров из алюминиевых и магниевых конструкционных сплавов на базе 106 циклов в 24 из 45 случаев несколько больше, чем на базе 107 циклов, и в 21 случае указанная характеристика оказалась несколько меньше на базе 106 циклов, чем на базе 107 циклов.
для гладких и надрезанных образцов различных размеров из алюминиевых и магниевых конструкционных сплавов на базе 106 циклов в 24 из 45 случаев несколько больше, чем на базе 107 циклов, и в 21 случае указанная характеристика оказалась несколько меньше на базе 106 циклов, чем на базе 107 циклов.
Дата добавления: 2015-08-08; просмотров: 835;
