Оценка параметров уравнения кривой усталости по результатам испытаний с возрастающей амплитудой цикла напряжений

Евстратовой С.П. [22] была показана возможность использования ускоренного метода испытания на усталость с возрастающей амплитудой цикла напряжений для оценки параметров уравнения кривой усталости Штромейера (1.3) и М.Н.Степнова (1.6).

Пусть скорость возрастания амплитуды цикла напряжений

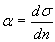(3.25)

Разрушение наступает при амплитуде напряжения 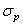и числе циклов n_p в момент, когда сумма накопленных повреждений достигает своего предельного значения

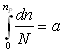(3.26)

Применительно к сталям и титановым сплавам с использованием уравнения Штромейера (1.3) в виде

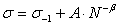(3.27)

будем иметь

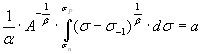(3.28)

где 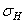— начальная амплитуда напряжений.

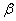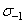Если принять, предельную сумму независимой от скорости возрастания амплитуды цикла напряжения (что подтверждается результатами испытаний углеродистых и легированных сталей, высокопрочного чугуна и деформируемых алюминиевых сплавов), то уравнение (3.28) можно использовать для определения параметров кривой усталости A, и . Для этой цели следует испытать три группы объектов при различных скоростях нагружения и по полученным значениям амплитуды разрушающих напряжений составить три уравнения по формуле (3.28). Четвертую группу образцов следует испытать при постоянном уровне амплитуды цикла напряжений.

Для деформируемых титановых, алюминиевых и магниевых сплавов с использованием уравнения кривой усталости М.Н.Степнова (1.6) в виде

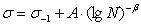(3.29)

и с учетом формул (3.25) и (3.26) получим

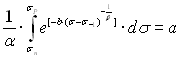, (3.30)

где .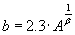

Опыт использования указанной методики позволяет сформулировать последовательность определения параметров уравнения кривой усталости.

Вначале из системы уравнений типа (3.28) и (3.30) определяют параметры 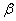и 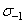. Далее по результатам усталостных испытаний нескольких образцов на высоком уровне амплитуды напряжения на основании уравнений кривой усталости (3.27) и (3.29) находят параметр A. При необходимости оценку предельной суммы накопленных повреждений можно произвести для найденных значений параметров A, 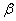и 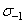по уравнениям (3.28) и (3.30).

Точность определения параметров уравнений кривой усталости практически соответствует точности, получаемой при обычных усталостных испытаниях такого же количества образцов, а время испытаний сокращается приблизительно в 10 раз.

Объем и время испытаний дополнительно сокращается на 20-30%, если для исследуемого объекта уже известна предельная сумма накопленных повреждений, которую можно определить, анализируя результаты ускоренных испытаний аналогичных материалов и элементов конструкций.

Рассмотренная методика позволяет производить оценку параметров уравнения кривых усталости как по окончательному разрушению, так и по образованию макротрещины усталости заданной протяженности. В последнем случае в уравнениях (3.28) и (3.30) в качестве 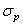принимается амплитуда напряжения, соответствующая появлению макротрещины усталости заданного размера.