Оценка параметров уравнения кривой усталости по результатам форсированных испытаний
Форсирование может осуществляться применением высокочастотных испытательных установок, а также путем испытаний образцов и элементов конструкций при напряжениях, существенно превышающих предел выносливости.
Применение высокочастотных испытательных установок (с частотой 1000 Гц и более) ограничено, так как в процессе испытаний на указанных частотах происходит интенсивный разогрев образцов, в связи с чем возникает необходимость их охлаждения, что искажает результаты испытаний. Кроме этого, рассматриваемый метод форсирования испытаний оказывается малопригодным для образцов с концентратором напряжений и образцов больших сечений. В первом случае — из-за локального разогрева материала в зоне концентратора, во втором — из-за чрезмерного возрастания мощности испытательных установок и наличия заметного градиента температуры по сечению элемента.
Известно, что основное машинное время затрачивается на испытания образцов или элементов конструкций при напряжении, равном или меньшем предела выносливости. Длительность испытаний можно значительно сократить, если ограничиться испытаниями образцов или элементов конструкций лишь при напряжениях, больших предела выносливости, а величину предела выносливости определять путем экстраполяции с помощью уравнения кривой усталости, параметры которого могут быть определены на основании испытаний при высоких уровнях напряжений. В этом заключается суть форсированных испытаний на усталость.
Следует иметь в виду, что приемлемая точность оценки предела выносливости форсированным методом испытания на усталость достигается в случае экстраполяции кривой усталости не более чем на один — два порядка по долговечности, а также при использовании достаточно обоснованных уравнений кривых усталости. Графическая же экстраполяция кривой усталости на один порядок по долговечности приводит к неприемлемой величине ошибки оценки предела выносливости.
Форсированный метод может быть использован для определения как характеристик сопротивления образованию трещины усталости, так и характеристик сопротивления усталостному разрушению.
Применительно к высокопрочным углеродистым и легированным сталям, а также для титановых сплавов, в качестве уравнения кривой усталости следует использовать уравнение Штромейера (1.3), которое в данном случае целесообразно представить в виде
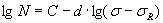 (3.20)
(3.20)
или
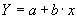 (3.21)
(3.21)
где 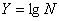 ,
, 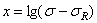 , a=C, b=-d.
, a=C, b=-d.
Параметры a и b уравнения (3.21) определяют методом наименьших квадратов по формулам (3.6)- (3.11), в которых m представляет собой число уровней напряжения при испытании на усталость, а ni – число образцов, испытанных на i-ом уровне напряжения. Оценку указанных параметров производят методом последовательных приближений. Для этого задаются рядом значений 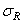 и для каждого значения оценивают параметры a и b, а также меру рассеяния Q экспериментальных точек вокруг линии (3.21) по формуле (3.12).
и для каждого значения оценивают параметры a и b, а также меру рассеяния Q экспериментальных точек вокруг линии (3.21) по формуле (3.12).
В качестве окончательной оценки параметра 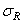 уравнения (3.20), представляющего собой предел неограниченной выносливости, принимают величину, которой соответствует минимальное значение Q. Для этого значения
уравнения (3.20), представляющего собой предел неограниченной выносливости, принимают величину, которой соответствует минимальное значение Q. Для этого значения 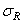 окончательно оценивают значения параметров уравнения (3.21). Схема оценки параметра
окончательно оценивают значения параметров уравнения (3.21). Схема оценки параметра 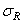 показана на рис. 3.5.
показана на рис. 3.5.
Вычисление предела ограниченной выносливости для выбранной базы производится по формуле (1.3) на основании найденных значений параметров C, d и 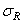 .
.
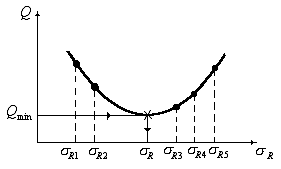
Рис. 3.5. Схема оценки параметра 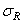 уравнения кривой усталости (3.20)
уравнения кривой усталости (3.20)
Точность метода тем выше, чем ближе нижний уровень напряжений при испытании к пределу ограниченной выносливости. Не рекомендуется экстраполяция опытных данных более чем на один — два порядка по долговечности. При выполнении этих условий погрешность метода составляет около 10% при десятикратном сокращении времени испытаний. Экономия в образцах практически отсутствует.
Для алюминиевых, магниевых и титановых сплавов в качестве уравнения кривой усталости принимают уравнение М.Н.Степнова (1.6) при N1=0. Для случая форсированных испытаний на усталость это уравнение целесообразно представить в виде
 (3.22)
(3.22)
или
 (3.23)
(3.23)
которое приводят к линейному
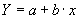 (3.24)
(3.24)
где 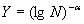 ,
, 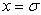 ,
, 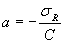 ,
, 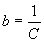 .
.
Оценку параметров уравнений (3.23) и (3.24) производят методом последовательных приближений. Для этого задаются рядом значений  , по формулам (3.6) - (3.11) вычисляют значения параметров уравнения (3.24), и по формуле (3.12) определяют меру рассеяния Q экспериментальных точек вокруг линии (3.24).
, по формулам (3.6) - (3.11) вычисляют значения параметров уравнения (3.24), и по формуле (3.12) определяют меру рассеяния Q экспериментальных точек вокруг линии (3.24).
В качестве оценки параметра  уравнения (3.23) принимают величину, которой соответствует минимальное значение Q. Для полученной величины
уравнения (3.23) принимают величину, которой соответствует минимальное значение Q. Для полученной величины  окончательно по формулам (3.6)- (3.11) вычисляют значения параметров уравнения (3.24), а затем и значения параметров уравнения кривой усталости (3.22) и (3.23).
окончательно по формулам (3.6)- (3.11) вычисляют значения параметров уравнения (3.24), а затем и значения параметров уравнения кривой усталости (3.22) и (3.23).
Схема оценки параметра  показана на рис. 3.6.
показана на рис. 3.6.
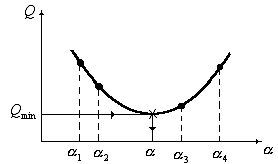
Рис. 3.6. Схема оценки параметра  уравнения кривой усталости (3.22) и (3.23)
уравнения кривой усталости (3.22) и (3.23)
Экстраполяция кривой усталости при числе испытанных образцов n = 8-10 на два порядка (от N=106циклов до N=108циклов) приводит к относительной средней квадратической ошибке, не превышающей 5-6%.
Этот подход был успешно апробирован и для натурных конструкций из деформируемых алюминиевых сплавов (бурильные трубы, лонжерон несущего винта вертолета, лонжерон хвостового винта вертолета, винт самолета и др.).
Дата добавления: 2015-08-08; просмотров: 677;
