Оценка коэффициента вариации предела выносливости по результатам испытаний на высоких уровнях амплитуды цикла напряжений

Принятие гипотезы о независимости коэффициента вариации предела ограниченной выносливости от базы испытаний на усталость создает возможность построения квантильных кривых усталости, если уже надежно построена медианная (средняя) кривая усталости и произведена оценка коэффициента вариации 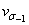. В этом случае будем иметь

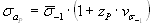, (4.6)

где 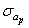- квантиль уровня P предельной амплитуды цикла напряжений для заданной долговечности, 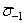- среднее или медианное значение предела выносливости (предельной амплитуды) для заданной долговечности, определяется по медианной кривой усталости (P=0.5), 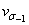- эмпирическое значение коэффициента вариации предела выносливости, z_p — квантиль уровня P нормального распределения.

Надежная оценка коэффициента вариации предела выносливости на основании стандартных испытаний на усталость требует испытаний большого числа образцов (n = 60...100), что не всегда выполнимо.

Однако, коэффициент вариации предела выносливости можно оценить на основании результатов испытания на усталость форсированным методом. Для этого на высоком уровне амплитуды цикла напряжений 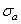подвергают испытаниям n = 15...25 образцов и по полученным результатам оценивают выборочную дисперсию величины 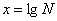по формуле

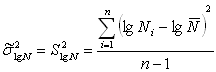. (4.7)

На основании теоремы о числовых характеристиках функции Y случайного аргумента x

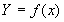(4.8)

математическое ожидание функции равно

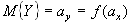(4.9)

где a_x — математическое ожидание случайного аргумента .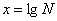

Дисперсия функции определяется как

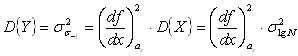(4.10)

Применительно к уравнению кривой усталости Штромейера (1.3) (стали, титановые сплавы), которое для рассматриваемого случая записывают в виде

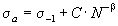(4.11)

с учетом (4.2) и (4.10) получают

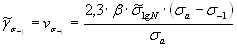(4.12)

или

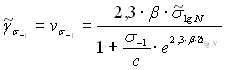(4.13)

Для деформируемых алюминиевых, титановых и магниевых сплавов с использованием уравнения кривой усталости СтепноваМ.Н. [1] в виде (3.22) и формул (4.2) и (4.10) получают оценки коэффициента вариации предела выносливости

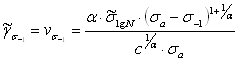(4.14)

или

(4.15)

Машинное время при форсированных испытаниях на усталость с целью оценки коэффициента вариации предела выносливости при удовлетворительной точности сокращается, примерно, в 100 раз, а число испытанных образцов – в 4 раза по сравнению со стандартными испытаниями на усталость.

Если по результатам испытаний на нескольких уровнях амплитуды цикла напряжений оценены соответствующие значения выборочного коэффициента вариации предела выносливости по формулам (4.12), (4.13) или (4.14), (4.15), то их объединяют в общую оценку

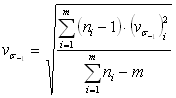(4.16)

где 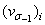— оценка коэффициента вариации предела выносливости, найденная по результатам испытаний образцов на i-м уровне амплитуды цикла напряжений (i = 1, 2, ..., m).

Принятие гипотезы о независимости коэффициента вариации предела выносливости от базы испытаний наряду с принятым видом уравнения кривой усталости дает возможность выразить зависимость степени рассеяния долговечности от уровня амплитуды цикла напряжений и средней долговечности на всем протяжении кривой усталости.

Применительно к кривой усталости Штромейера (4.11)

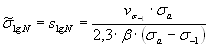(4.17)

и

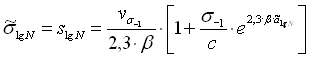(4.18)

При использовании уравнения кривой усталости Степнова М.Н. (3.22) получают

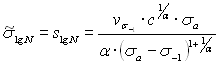(4.19)

и

(4.20)

Теоретически обоснованные уравнения (4.17)...(4.20) носят более общий характер по сравнению с эмпирически обоснованными уравнениями (4.3) и (4.4).

Зависимости (4.17)...(4.20) подвергались экспериментальной проверке для алюминиевых сплавов различных марок (АД33, АВ, Д16, В95 и др.). Для всех рассмотренных случаев соответствие указанных уравнений опытным данным вполне удовлетворительное. Несколько лучшее соответствие имеют уравнения (4.19) и (4.20), дающие близкие результаты с уравнениями (4.3) и (4.4).