Построение кривой распределения предела выносливости по результатам испытаний на усталость с возрастающей амплитудой цикла напряжений

Анализ кривых распределения разрушающих амплитуд цикла напряжений, приведенных в качестве примера на рис. 4.4 для сплавов АВ и МЛ5 (для других легких сплавов и сталей они имеют аналогичный вид), показал, для каждого материала и типа образцов при различных скоростях возрастания амплитуды цикла напряжений форма и наклон кривых распределения одинаковы, а различаются лишь медианные значения разрушающих амплитуд. Это позволяет по результатам ускоренных испытаний оценивать не только медиану предела выносливости и его дисперсию, но и производить оценку квантильных значений предела выносливости и строить эмпирическую функцию распределения [1].

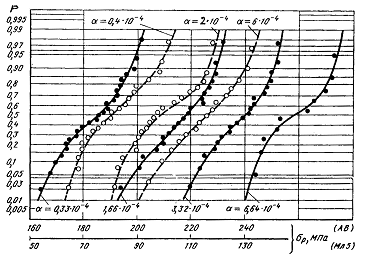
Рис. 4.4 Кривые эмпирических распределений разрушающих амплитуд напряжений для алюминиевого сплава АВ (сплошные линии, верхняя шкала 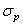) и магниевого сплава МЛ5 (штриховые линии, нижняя шкала ).

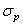Для этого все результаты ускоренных испытаний для рассматриваемого материала и типа образцов (m выборок) объединяют в одну общую совокупность путем введения случайной величины — отклонения от медианы

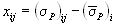, (4.30)

где - оценка медианы разрушающей амплитуды цикла напряжений при i-ой скорости нагружения; - j-й член вариационного ряда разрушающей амплитуды цикла напряжений при i-ой скорости нагружения.

Далее строят общий вариационный ряд из значений x_ij и наносят на нормальной вероятностной сетке график эмпирической функции распределения величиныx_ij. Подобные обобщенные кривые распределения для ряда сплавов приведены на рис. 4.5.

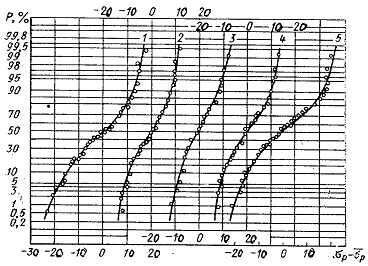
Рис. 4.5 Обобщенные кривые распределения отклонений разрушающих амплитуд цикла напряжений от среднего значения:
1. — Сплав АВ (Cu – 0,46%, Mn – 0,25%), n=75;
2. — Сплав типа АВ (Cu – 0,010%, Mn – 0,60%), n=90;
3. — Сплав типа АВ (Cu – 0,095%, Mn – 0,28%), n=50;
4. — Сплав типа АВ (Cu – 0,04%, Mn – 0,12%), n=60;
5. — Сплав МЛ5, n=55.

Характер кривых распределения разрушающих амплитуд цикла напряжений (см. рис. 4.4) и отклонений от медианы (см. рис. 4.5) свидетельствует о существовании нижней и верхней границ разрушающих амплитуд. Преобразование распределения путем введения нижней границы разрушающих амплитуд 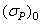и верхней границы 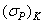приводит распределение случайной величины 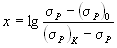к нормальному (рис. 4.6).

Значение нижней границы 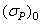зависит от скорости возрастания амплитуды напряжений, однако разность 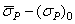так же, как и 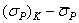, для каждого сплава является устойчивой величиной, не зависящей от скорости возрастания амплитуды и уровня начального напряжения.

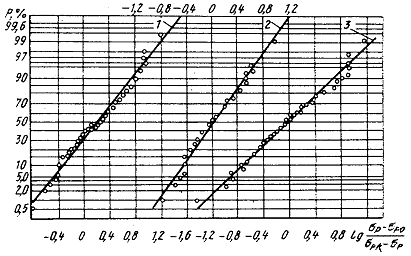
Рис. 4.6 Преобразование распределения путем введения верхней и нижней границ разрушающих напряжений:
1. — Сплав АВ (Cu – 0,46%, Mn – 0,25%), 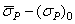=30МПа, 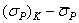=20МПа;
2. — Сплав типа АВ (Cu – 0,095%, Mn – 0,28%), 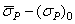=15МПа, 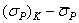=15МПа;
3. — Сплав МЛ5, 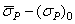=22МПа, 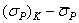=23МПа.

Квантили предела выносливости 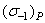для уровня вероятности P находят из выражения

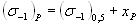, (4.31)

где x_p — оценка квантиля величины x_ij, определяемая по графику эмпирической функции распределения (рис. 4.5); 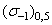- оценка медианы предела выносливости, определяемая по формуле (3.1).

Произведя вычисления по формуле (4.31) для нескольких уровней вероятности P, строят эмпирическую функцию распределения предела выносливости. Расчет значений предела выносливости образцов из алюминиевых и титановых сплавов для базы, отличной от 10⁷ циклов, производят с помощью уравнений соответственно (2.38) и (2.43).

На рис. 4.7в качестве примера сопоставлены эмпирические кривые распределения пределов ограниченной выносливости сплавов АВ и МЛ5, построенные по результатам обычных и ускоренных испытаний. Приведенные данные показывают удовлетворительное соответствие характеристик сопротивления усталости, найденных указанными методами. Расхождения в пределах выносливости не превышают 5.8МПа. Аналогичные результаты имеют место и для других марок алюминиевых сплавов, а также для углеродистой и легированной сталей.

Рис. 4.7 Сопоставление кривых эмпирических распределений пределов ограниченной выносливости, найденных ускоренным (сплошные линии) и обычным (штриховые линии) методами
1. — Сплав МЛ5, N_б=10⁷ циклов;
2. — Сплав АВ, N_б=10⁸ циклов;
3. — Сплав АВ, N_б=10⁷ циклов.

Как уже отмечалось, при использовании метода Про для оценки медианы предела выносливости требуется такое же число образцов, как и при обычных испытаниях. Однако, при построении кривой распределения предела выносливости ускоренным методом с возрастающей амплитудой цикла напряжений в связи с возможностью объединения отдельных выборок в единую совокупность для сплавов со стабильными усталостными свойствами число объектов должно составлять лишь 30 - 40, а для сплавов с повышенной дисперсией усталостных свойств 40 - 60 штук. Случайная ошибка оценки квантили предела выносливости для малых уровней вероятностей будет такой же, как и при обычном методе испытаний 100 - 150 образцов. Таким образом, при построении кривой распределения предела выносливости наряду с 10 - 50-кратным сокращением машинного времени достигается двух-трехкратная экономия объектов испытаний.

Рассмотренная выше методика позволяет производить оценку характеристик рассеяния усталостных свойств как по окончательному разрушению, так и по образованию макротрещины усталости определенного размера.