Решение. Поперечное сечение представляет собой равнобедренный треугольник, а следовательно, ось у – ось симметрии и центр тяжести рассматриваемого поперечного сечения
Поперечное сечение представляет собой равнобедренный треугольник, а следовательно, ось у – ось симметрии и центр тяжести рассматриваемого поперечного сечения лежит на этой оси.
Для нахождения центра тяжести используем формулу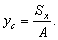 
Запишем
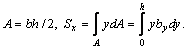(а)
Из подобия треугольников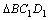 
и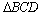 
находим
или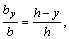 
откуда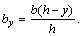 
Найденное значение by подставляем в формулу (а) для вычисления статического момента Sx:
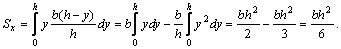
В этом случае формула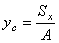 
дает
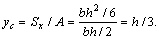
На рисунке проводим линию у = ус = h/3. Центр тяжести треугольного поперечного сечения будет лежать на пересечении проведенной линии и оси у. Координаты центра тяжести этого сечения: х = 0, у = h/3.
Ответ: xc = 0, yc = 4R/(3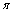 
).
Дата добавления: 2015-08-08; просмотров: 709;