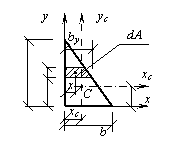
Пример 13. Определить осевые моменты инерции Ix, Iy прямоугольного треугольника относительно случайных осей х, у (см
Определить осевые моменты инерции Ix, Iy прямоугольного треугольника относительно случайных осей х, у (см. рис.). Вычислить положение центра тяжести. Найти значения осевых моментов инерции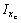 
, 
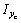и центробежный момент инерции 
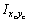относительно центральных осей хс, ус, проходящих через центр тяжести С. Определить расположение главных осей инерции поперечного сечения в форме сплошного прямоугольного треугольника.
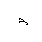
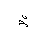
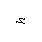
Указания. Для нахождения центробежного момента инерции 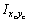можно использовать формулы 
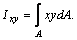и 
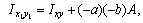которые для рассматриваемого случая принимают вид:
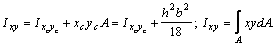
Из подобия треугольников находим (см. рис.):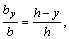 
откуда 
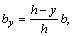следовательно, площадь элементарной площадки dA будет
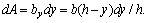
Горизонтальная координата х центра тяжести элементарной площадки dA определяется как x = by /2 =b (h – y)/(2h).
Подставим значения х и dA в формулу для определения Ixy:
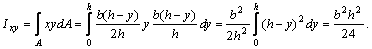
Переходим к центральным осям хс и ус, для которых
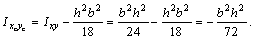
Ответ: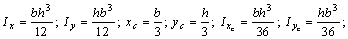 
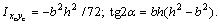
Дата добавления: 2015-08-08; просмотров: 951;