Ток вероятности

Плотность вероятности обнаружения частицы около точки r

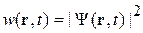
зависит от времени. Вероятность обнаружить частицу во всем пространстве неизменна

.

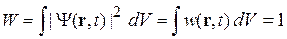Следовательно, вероятность перетекает из одного места в другое. Вводится плотность тока вероятности 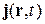и соответствующий оператор.

Умножая плотность тока вероятности j на заряд частицы e, получаем плотность электрического тока

,

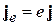вызванного движением частицы. В теории электрического тока многих частиц

,

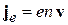где 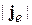– заряд, проходящий за 1с через единичное поперечное сечение проводника; n – концентрация частиц. Тогда плотность тока вероятности для одной частицы

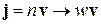
выражается через скорость.

Плотность тока вероятности. Используем оператор скорости

,

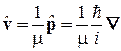где

.

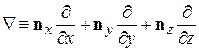Для частицы в состоянии 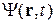определяем плотность тока вероятности

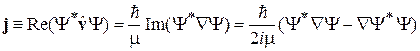, (2.71)

где учтено

.

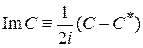Вектор выражаем через декартовы компоненты

,

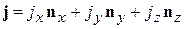где

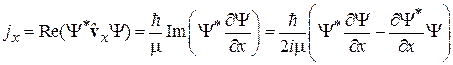. (2.72)

Уравнение непрерывности тока вероятности. Используем

,

.

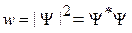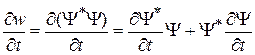Из уравнения Шредингера (2.54)

,

,

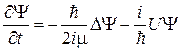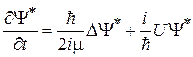тогда

.

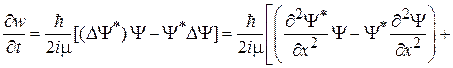
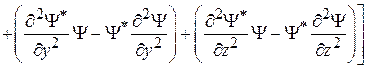Используем (2.72)

,

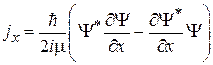тогда первая круглая скобка равна 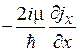и аналогично для остальных скобок. В результате получаем уравнение непрерывности

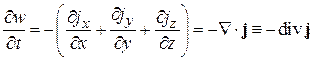, (2.73)

где divj – дивергенция плотности тока является потоком из единичного объема. Согласно (2.73) поток из объема уменьшает вероятность в этом объеме. Следовательно, уравнение Шредингера описывает систему, у которой нет источников и стоков частиц.

Ток вероятности для частицы с импульсом р в состоянии плоской волны

.

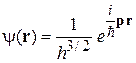Плотность вероятности

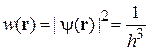
распределена равномерно по всему пространству. В состоянии равномерного движения частица обнаруживается в любой точке пространства с равной вероятностью.

Из (2.72)

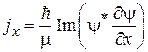
находим

,

.

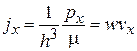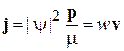Плотность электрического заряда и тока для частицы с зарядом е равны

,

.

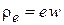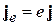При равномерном движении заряда используем 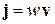и получаем известное соотношение

.

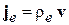Из уравнения непрерывности (2.73) следует закон сохранения заряда в дифференциальной форме

.

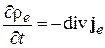Ток вероятности в стационарном состоянии. Используем (2.63)

,

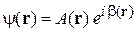где A и β – вещественные, тогда

.

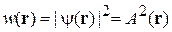Вычисляем плотность тока вероятности (2.71)

.

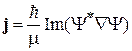Учитываем

,

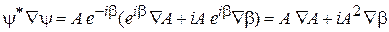получаем

.

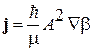Используя

, ,

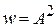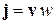находим

,

,

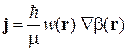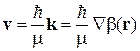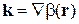. (2.74)

Для стационарного состояния волновой вектор равен градиенту фазы волновой функции, плотность тока вероятности пропорциональна плотности вероятности и градиенту фазы волновой функции. Если фаза b в разных точках одинаковая, то , .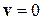

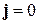Выполняется

.

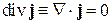Для стационарного состояния поток вероятности из любого объема равен нулю.