Уравнение Шредингера
Для частицы, описываемой гамильтонианом 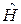 , волновая функция
, волновая функция 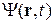 находится из уравнения, которое получил Эрвин Шрёдингер в 1926 г. Если потенциальная энергия не зависит от времени, то полная энергия Е постоянна, зависимости от координат и времени в волновой функции разделяются
находится из уравнения, которое получил Эрвин Шрёдингер в 1926 г. Если потенциальная энергия не зависит от времени, то полная энергия Е постоянна, зависимости от координат и времени в волновой функции разделяются 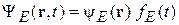 , где
, где 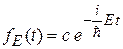 . Функция
. Функция 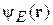 находится из стационарного уравнения Шредингера.
находится из стационарного уравнения Шредингера.
Правило соответствия. При переходе от классической к квантовой теории физическим величинам сопоставляются эрмитовые операторы. При этом соотношения между динамическими характеристиками сохраняются. Это обеспечивает совпадение результатов теорий при больших значениях квантовых чисел.
Оператор Гамильтона. Гамильтониан частицы в классической теории является суммой кинетической и потенциальной энергий, выраженных через импульсы и координаты:
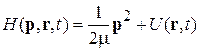 .
.
Переходим к операторам
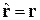 ,
,
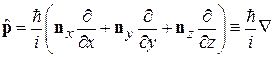 ,
,
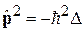 ,
,
где
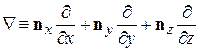 – оператор градиента,
– оператор градиента,
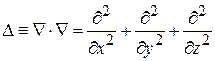 – оператор Лапласа.
– оператор Лапласа.
Получаем оператор полной энергии, или оператор Гамильтона
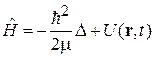 . (2.53)
. (2.53)
Волновое уравнение Шредингера следует из (2.52)
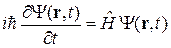
и (2.53) в виде
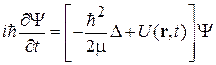 . (2.54)
. (2.54)
Стационарное уравнение Шредингера. Если потенциальная энергия не зависит от времени
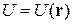 ,
,
то полная энергия E сохраняется и состояние системы стационарное. В (2.54) слагаемые с координатами и временем разделены, решение ищем в виде
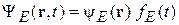 . (2.55)
. (2.55)
Подставляем (2.55) в (2.54), умножаем уравнение слева на  , переменные разделяются
, переменные разделяются
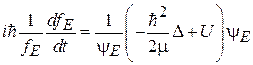 .
.
Левая и правая стороны зависят от разных переменных, поэтому они равны постоянной Е.
В уравнении
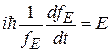
разделяем переменные
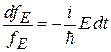 ,
,
интегрируем и находим
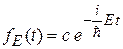 . (2.56)
. (2.56)
Для 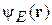 получаем стационарное уравнение Шредингера
получаем стационарное уравнение Шредингера
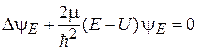 . (2.57)
. (2.57)
Уравнение (2.57) с учетом 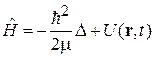 является уравнением для собственной функции оператора гамильтона
является уравнением для собственной функции оператора гамильтона
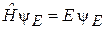 , (2.58)
, (2.58)
следовательно, Е – полная энергия. Если система одномерная, то для 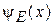 из (2.57) получаем
из (2.57) получаем
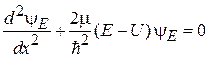 . (2.59)
. (2.59)
Стационарное состояние с энергией E имеет вид
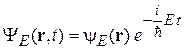 . (2.60)
. (2.60)
Функция периодически зависит от времени как 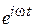 с частотой, пропорциональной энергии:
с частотой, пропорциональной энергии:
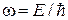 . (2.61)
. (2.61)
Для свободной частицы при 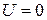 получаем зависимость частоты от волнового числа – закон дисперсии
получаем зависимость частоты от волнового числа – закон дисперсии
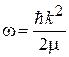 . (2.61а)
. (2.61а)
Координатная часть волновой функции стационарного состояниявыражается через вещественные функции – амплитуды A и фазы β
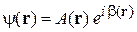 . (2.63)
. (2.63)
Плотность вероятности
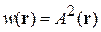 .
.
Дата добавления: 2015-08-08; просмотров: 744;
