СоотношениЕ неопределенностей

Для измерения величины a, описываемой оператором 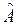, частица в исследуемом состоянии 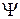приводится во взаимодействие с соответствующим прибором. Его состояние, описываемое классической физикой, изменяется. Регистрируем изменение и получаем измеряемую величину. Повторяем измерение N раз, находим среднее значение и дисперсию

,

.

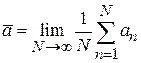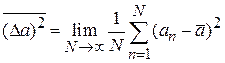Если исследуемое состояние совпадает с одной из собственных функций оператора 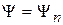, то результат измерения однозначен и погрешность равна нулю

, .

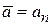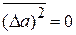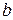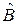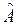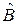Для измерения величины , описываемой оператором , используется другой прибор. Если и коммутируют, то наборы их собственных функций {Ψ_n} совпадают, соответствующие измерения совместимы. В состоянии 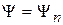результаты однозначные 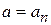, , 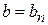их точность не ограничена.

Если эрмитовые операторы 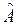и 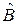не коммутируют

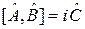, (2.29)

где 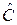– эрмитовый оператор (доказательство на практических занятиях), то 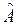и 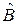имеют разные наборы собственных функций. Измерительные приборы для а и b несовместимы, действие одного прибора нарушает работу другого. Например, на лекции 1 показано, что при измерении координаты волны используется экран со щелью. Это вызывает дифракцию волны и растет неопределенность импульса. Измерить а и b одновременно с высокой точностью невозможно. В состоянии 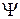найдем связь между их флуктуациями, т. е. абсолютными погрешностями:

,

,

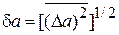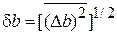где дисперсия по определению среднего равна

,

.

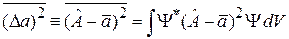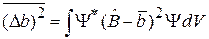Ограничение коммутатора. Среднее от квадратичной формы эрмитовых операторов 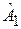и 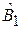по любому состоянию Ψ не может быть отрицательным

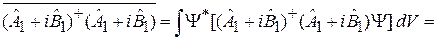
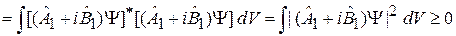. (2.30)

Во втором равенстве использована операция эрмитового сопряжения. Упрощаем левую сторону (2.30), учитывая эрмитовость операторов:

.

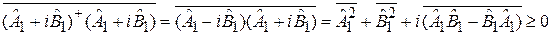В результате коммутатор

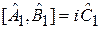
ограничен

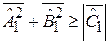. (2.31)

Соотношение неопределенностей Гейзенберга. В качестве 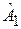и 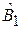выбираем операторы относительного отклонения от среднего

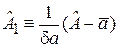, , (2.32)

удовлетворяющие

.

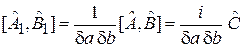С учетом

,

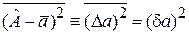находим

, , .

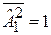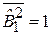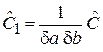Из (2.31) получаем

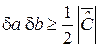. (2.33)

Если операторы коммутируют, то 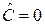, 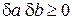и измерения a и b можно выполнить с неограниченной точностью.

Соотношение неопределенностей координата-импульс. Коммутатор

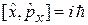
сравниваем с (2.29)

,

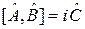получаем

, ,

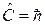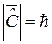из (2.33) находим

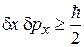(2.37)

– чем точнее измеряется координата частицы, тем неопределеннее импульс, и наоборот. Локализация частицы приводит к увеличению неопределенности ее импульса и кинетической энергии. Аналогичная формула была получена в полуклассической квантовой механике.

Соотношение неопределенностей энергия-время. Средняя скорость частицы выражается через путь и время

.

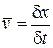Флуктуация кинетической энергии

,

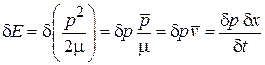тогда

.

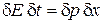Учитывая (2.37), находим

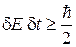(2.39)

– чем точнее измеряется энергия, тем больший промежуток времени необходим для измерения;

– чем уже энергетический уровень δЕвозбужденного состояния, тем больше время его жизниδt.