Прямые, обратные и дополнительные коды чисел с фиксированной запятой

ЭВМ выполняет арифметические операции над числами с фиксированной запятой в машинных кодах. Простейшим машинным кодом является прямой код.

Прямой код числа Х аналогичен двоичному коду, но число его разрядов строго определено и положение двоичной точки в самом коде никак не указано.

Прямые коды чисел просты, но плохо приспособлены для выполнения операций алгебраического сложения и вычитания чисел. Проще и быстрее выполняются операции алгебраического суммирования, вычитания и деления в дополнительных или обратных кодах.

Дополнительный код двоичного числа Х, представленного в n-разрядной сетке, определяется как

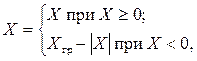
где Х_гр – величина, равная весу разряда, следующего за старшим разрядом используемой разрядной сетки. Для правильных дробей Х_гр=2, для целых чисел Х_гр=2ⁿ.

Таким образом, дополнительный код положительного числа совпадает с прямым кодом, а дополнительный код отрицательного числа получается как дополнение до граничного числа.

Обратный код двоичного числа Х, представленного в n-разрядной сетке, определяется как

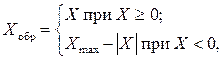
где Х_max – величина наибольшего числа без знака, размещающегося в n‑разрядной сетке. Для правильных дробей Х_max=2–2^–n+1, для целых чисел Х_max=2ⁿ–1.

Граничное значение Х_гротличается от максимального зна­чения Х_maxна одну единицу младшего разряда (мл. р.):

Х_гр = Х_max +1 мл. р.

Для положительных чисел прямой, обратный и дополнительный коды совпадают.

В случае отрицательных чисел дополнительный и обратный коды связаны между собой соотношением:

Х_доп = Х_обр +1 мл. р.

Правило представления двоичного числа в обратном коде:

1) представить двоичное число в прямом коде в n-разрядном формате. Если число положительное, то его прямой и обратный коды совпадают и больше ника­ких преобразований делать не надо;

2) если число отрицательное, то в старшем (знаковом) разряде надо оставить 1, а в цифровых разрядах все цифры изменить на инверсные, то есть вместо 0 записать 1 и вместо 1 записать 0.

Правило представления двоичного числа в дополнительном коде:

1) представить двоичное число в прямом коде в n-разрядном формате. Если число положительное, то на этом представление числа и заканчивается, так как прямой, обратный и дополнительный коды в этом случае совпадают;

2) если число отрицательное, то перейти от его прямого кода к обратному;

3) прибавить к обратному коду отрицательного числа единицу младшего разряда.

Правило преобразования дополнительного кода в прямой код:

1) если в старшем (знаковом) разряде стоит 0, то число положительное и прямой код совпадает с дополнительным;

2) если в старшем разряде стоит 1, то число отрицательное, поэтому из до­полнительного кода числа надо вычесть 1 младшего разряда с целью получения обратного кода числа, затем заменить все 0 на 1 и 1 на 0 в цифровых разрядах об­ратного кода, а в знаковом разряде оставить 1.

Прямой код из дополнительного кода отрицательного числа можно получить и по-другому: в знаковом разряде оставить 1, все цифровые разряды инвертировать и к полученному проме­жуточному результату прибавить единицу младшего разряда. Дополнительные и обратные коды чисел с фиксированной запятой (точкой) упрощают и ускоряют выполнение арифметических операций в ЭВМ.

Пример 1. Представить в 8-разрядном формате прямые, обратные и дополнительные коды целых двоичных чисел: Х₁ = 1011; Х₂ = –1011; Х₃ = 11 0110; Х₄ = –11 0110. Найти десятичные эквиваленты заданных чисел.

Решение

Х₁ = 1011₍₂₎ = 0000 1011_{(пр)(обр)(доп)} = 11₍₁₀₎;

Х₂ = –1011₍₂₎ = 1000 1011_(пр) = 1111 0100_(обр) = 1111 0101_(доп) = –11₍₁₀₎;

Х₃ = 11 0110₍₂₎ = 0011 0110_{(пр)(обр)(доп)} = 54₍₁₀₎;

Х₄ = –11 0110₍₂₎ = 1011 0110_(пр) = 11001001_(обр) = 11001010_(доп) = –54₍₁₀₎.

Пример 2. Представить в 8-разрядном формате прямые, обратные и дополнительные коды дробных двоичных чисел, найти их десятичные эквиваленты: Х₁ = –0,11; Х₂ = –0,1101; Х₃ = 0,0101; Х₄ = 0,10101.

Решение

Х₁ = –0,11₍₂₎ = 11100000_(пр) = 10011111_(обр) = 10100000_(доп) = – (0,5+0,25) = =–0,75;

Х₂ = –0,1101₍₂₎ =11101000_(пр) = 10010111_(обр) = 10011000_(доп) =

=–(0,5+0,25+0,0625) = –0,8125;

Х₃ = 0,0101₍₂₎ = 00101000_{(пр)(обр)(доп)} = 0,3125₍₁₀₎;

Х₄ = 0,10101₍₂₎ =01010100_{(пр)(обр)(доп)} = 0,65625₍₁₀₎.

Пример 3. Числа представлены как целые в дополнительных кодах: Х₁ =10111101_(доп); Х₂ = 00101010_(доп). Найти десятичные эквиваленты.

Решение

Необходимо найти прямые коды чисел, после чего перевести их в десятичные числа.

Число Х₁ отрицательное, следовательно, необходимо перевести его из дополнительного кода в обратный вычитанием одной единицы младшего разряда, затем в прямой код инверсией всех цифровых разрядов и далее в отрицательное двоичное число.

Х₁ =10111101_(доп) = 10111100_(обр) = 11000011_(пр) = –1000011₍₂₎ = –67₍₁₀₎.

Число Х₂ положительное, следовательно, его прямой код совпадает с дополнительным кодом:

Х₂ = 00101010_(доп) = 101010_(пр) = 2+8+32 = 42₍₁₀₎.