Представление чисел с плавающей запятой

Число в нормальной форме может быть записано как

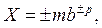
где m – мантисса числа;

b – основание системы счисления;

p – порядок числа.

Для задания числа в нормальной форме (НФ) необходимо задать знаки мантиссы и порядка, основание системы счисления и модули мантиссы и порядка в заданной системе счисления. Поскольку взаимное изменение мантиссы и порядка приводит к изменению положения b-ичной запятой в записи числа, то НФ получила название форма с плавающей запятой.

В памяти машины числа с плавающей запятой можно записывать без значения b:

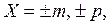
так как основание системы счисления не меняется от числа к числу, и поэтому нет смысла хранить избыточную информацию.

Записи числа по этому выражению соответствует формат, который принято называть классическим форматом чисел с плавающей точкой. Он состоит из четырех полей: знака мантиссы, мантиссы, знака порядка, порядка (рис.).

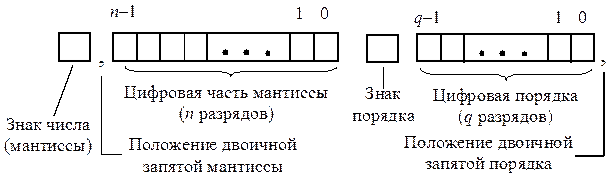
Мантисса и порядок в классическом формате представления хранятся в памяти ЭВМ в прямом коде.

Число, у которого абсолютная величина мантиссы удовлетворяет условию

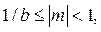
называется нормализованным.

Благодаря нормализации устраняются старшие нули мантиссы. Такую нормализацию называют нормализацией справа. Это обеспечивает максимальное количество значащих цифр мантиссы при ее фиксированной длине. При этом повышается точность вычислений и упрощаются действия над порядками и мантиссами. Перед записью в память числа нормализуют.

В процессе вычислений возможно появление одного или нескольких нулей в старших разрядах мантиссы, то есть денормализация мантиссы. Денормализация мантиссы устраняется сдвигом мантиссы влево с соответствующим уменьшением величины порядка. В освободившиеся младшие разряды мантиссы записывают нули.

Примеры:

а) в десятичной системе счисления

372,95 = 0,37295×10³;

25 = 0,025×10³ = 0,25×10²;

0,0000015 = 1,5×10^–6 = 0,15×10^–5 =0,015×10^–4;

б) в двоичной системе счисления

11010,1101 = 0,0110101101×2⁶ = 0,110101101×2⁵;

0,011011 = 0,11011×2^–1.

Нормализованная мантисса в двоичной системе счисления всегда представляется десятичным числом m в диапазоне 0,5£m<1.

При выполнении арифметических операций над числами, представленными в формате с плавающей запятой, надо отдельно выполнять их для порядков и мантисс. При алгебраическом сложении чисел надо сначала уравнять порядки слагаемых. При умножении порядки надо складывать, а мантиссы перемножать. При делении из порядка делимого вычитают порядок делителя, а над мантиссами совершают обычную операцию деления. После выполнения операций необходимо провести нормализацию результата, если это необходимо, что приводит к изменению порядков, так как каждый сдвиг на один разряд влево соответствует уменьшению порядка на единицу, а сдвиг вправо – увеличению его на единицу. Введение термина «плавающая запятая» как раз и объясняется тем, что двоичный порядок, определяющий фактическое положение запятой в изображении числа, корректируется после выполнения каждой арифметической операции, т. е. запятая в изображении числа плавает (изменятся ее положение) по мере изменения данной величины. А в изображении чисел с фиксированной запятой запятая жестко зафиксирована в определенном месте.

Арифметические операции с числами в форме плавающей запятой намного сложнее таких же операций для чисел с фиксированной запятой. Но зато плавающая запятая позволяет производить операции масштабирования автоматически в самой машине и избавляет от накопления абсолютной погрешности при вычислениях (хотя не избавляет от накопления относительной погрешности).