Перевод дробных чисел из одной позиционной системы в другую
Предположим, что правильное дробное число Х уже переведено в новую позиционную систему счисления с основанием b. Тогда число Х может быть записано в виде
X=a–1b–1 + a–2b–2 +…+ a–mb–m.
Умножим левую и правую части этого выражения на основание системы счисления b:
X·b=a–1+(a–2b–1 +a–3b–2+…+ a–mb–m+1).
В правой части этого выражения есть целая часть a–1 и дробная часть, заключенная в скобки. Таким образом, после первого умножения дробного числа Х на основание системы счисления получили первую цифру числа Х в новой системе счисления.
Умножим теперь часть последнего выражения, стоящую в скобках, на основание b новой системы счисления. Получим:
(a–2b–1 +a–3b–2+…+ a–mb–m+1)·b= a–2+(a–3b–1 +a–4b–2+…+ a–mb–m+2).
В правой части выражения снова имеем целую и дробную части. Получили вторую цифру a–2 числа Х в новой системе счисления.
Продолжая процесс умножения на основание системы счисления, получим все цифры переведенного числа с требуемой степенью точности. Все умножения выполняются в исходной системе счисления.
Пример 6. Перевести из десятичной системы счисления в двоичную дробное число 0,34375, ограничиваясь шестью знаками.
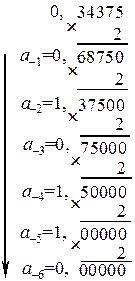
Ответ: Х=0,34375(10)=0,010110(2). Проверка: 010110(2)=0×2–1 + 1×2–2 + 0×2–3 +
+ 1×2–4 + 1×2–5 + 0×2–6=1/4 + 1/16 + 1/32 = 0,25 + 0,0625 +0,03125 = 0,34375(10). Получился точный ответ.
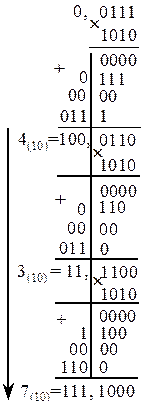 |
Пример 7. Перевести число Х=0,0111 из двоичной системы в десятичную с тремя знаками после десятичной запятой.
Ответ: 0,0111(2) =0,437(10). Получился неточный ответ, т. к. в дробной части последней строки не все цифры нулевые. Точный ответ: 0,0111(2) =0,4375(10).
В этом примере перевод двоичного числа в десятичную систему счисления сводится к умножению дробной части на основание системы счисления 1010(2)=10(10). Нам неудобно делать вычисления в недесятичной системе. Поэтому на практике перевод чисел из недесятичной системы счисления в десятичную сводится к подсчету суммы произведений степеней основания на соответствующую цифру, как это сделано в примере 5. При этом расчеты ведутся в десятичной системе счисления.
Перевод числа в данном примере: 0,0111(2) = 0×2–1+1×2–2+1×2–3+1×2–4 = =0,25+0,125+0,0625=0,4375(10).
Дата добавления: 2015-08-08; просмотров: 1052;
