Перевод целых чисел из одной позиционной системы в другую
Предположим, что число X уже переведено в новую систему счисления, тогда в позиционной системе счисления с основанием b оно может быть записано в виде
X=an–1bn–1 + an–2bn–2 +…+ a1b + a0.
Разделим левую и правую части этого выражения на основание b. Получим
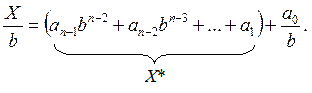
В этом выражении есть целая часть X*, заключенная в скобки, и первый остаток a0.
Разделив целую часть X* на основание системы счисления b, получим второй остаток a1. Повторяя процесс деления n раз, получим цифры числа, представленного в системе счисления с основанием b. Все операции необходимо выполнять в исходной системе счисления.
Пример 1. Перевести десятичное число 92 в двоичную систему счисления (b=2).
Решение.

Таким образом, 92(10)=1011100(2). Проверка: 1011100(2)=26+24+23+22=92(10).
Пример 2. Переведем двоичное число Х=1011100 в десятичную систему счисления. Выразим основание новой системы счисления через исходную систему: b=10(10)=1010(2).
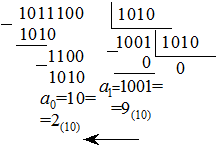
Это десятичное число 92.
Пример 3: Перевести двоичное число 11101011 в десятичное.
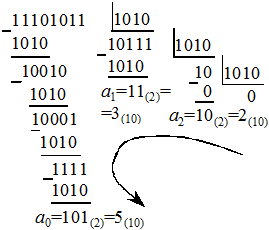
Получилось X=11101011(2) =235(10).
Пример 4. Перевести десятичное число Х=983 в восьмеричную систему счисления.
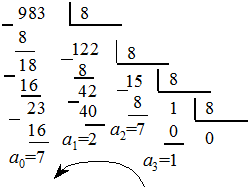
X=983(10)=1727(8).
Пример 5. Перевести десятичное число 42936 в шестнадцатеричное число.
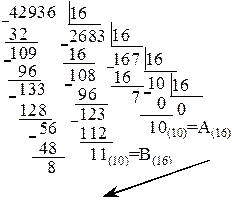
Ответ: 42936(10)=A7B8(16).
Дата добавления: 2015-08-08; просмотров: 1244;
