Прямой и обратный перевод из двоичной в восьмеричную и шестнадцатеричную системы счисления
ЭВМ производит арифметические и логические операции над исходными числами (операндами) в двоичной системе счисления, которая называется основной. Запись чисел в двоичной системе громоздка и неудобна для человека, поэтому при записи программ широко применяются вспомогательные восьмеричная и шестнадцатеричная системы счисления. Основаниями этих систем счисления являются целые степени числа 2. Это значительно облегчает перевод их в двоичный код.
Для перевода чисел из двоичной системы счисления в систему счисления с основанием 2k необходимо разбить исходное двоичное число на группы по k разрядов, начиная от запятой (вправо и влево). Каждая из этих групп рассматривается как целое число и заменяется одной цифрой в соответствии с таблицей 2. При переводе из двоичной системы счисления в восьмеричную число разбивается на триады, а при переводе в шестнадцатеричную – на тетрады.
Пример 9. Перевести число Х из двоичной системы в восьмеричную.
X=10010101010100,01101001.
Разбиваем разряды исходного числа на триады. При разбиении в неполные группы справа и слева дописываются нули:
X=010 010 101 010 100, 011 010 010.
Теперь заменяем каждую группу восьмеричной цифрой в соответствии с таблицей 2. Получаем
X=22524,322(8).
Пример 10. Перевести число Х из двоичной системы в шестнадцатеричную.
X=10010101010100,01101001.
X=0010 0101 0101 0100, 0110 1001=2554,69(16).
Пример 11. Перевести число Х из двоичной системы в шестнадцатеричную.
X=1100111011010,1011111010.
Разбиваем число на тетрады:
X=0001 1001 1101 1010, 1011 1110 1000=19DA,BE8(16).
Двоичная система счисления может использоваться как промежуточная при переводе чисел из восьмеричной в шестнадцатеричную систему и обратно.
Пример 12. Перевести число X=37520,610342 из восьмеричной системы в шестнадцатеричную, используя двоичную систему в качестве промежуточной.
Переводим исходное число в двоичную систему счисления путем замены каждой восьмеричной цифры в группу из трех двоичных разрядов (триаду):
X=37520,610342(8)=011 111 101 010 000, 110 001 000 011 100 010(2).
Разбиваем полученное двоичное число на тетрады:
X=011111101010000,110001000011100010=0011 1111 0101 0000,1100 0100 0011 1000 1000.
Заменяем каждую тетраду одной шестнадцатеричной цифрой. Получим
X=3F50,C4388(16).
При ручном переводе чисел из десятичной системы счисления в двоичную часто удобнее сначала перевести число в восьмеричную систему счисления, а затем из восьмеричной – в двоичную, чем выполнять перевод десятичного числа сразу в двоичную систему.
Пример 13. Перевести десятичное число 92 в двоичную систему счисления.
Переводим число в восьмеричную систему.
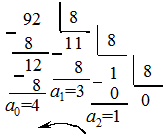
92(10)=134(8)
Переводим восьмеричное число в двоичное заменой каждой восьмеричной цифры двоичной триадой.
134(8)=001 011 100=1011100.
Существуют и другие способы перевода чисел из одной позиционной системы счисления в другую.
Дата добавления: 2015-08-08; просмотров: 2987;
